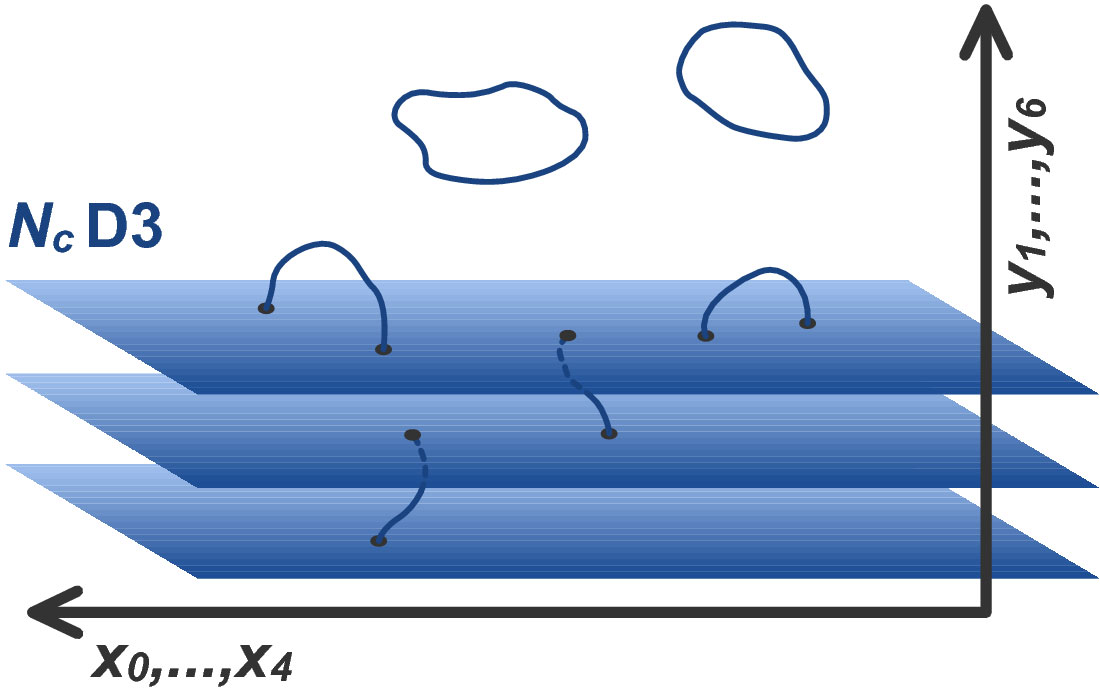
I listed the 4 essential properties of D3-branes, namely: i)…
D3-Brane Actions And Gaillard-Zumino Conditions With An SO(2) Duality For SuperGravity
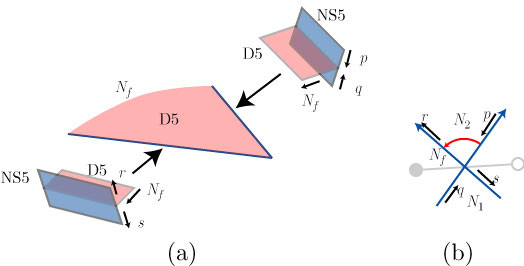
I last derived the D3-brane effective action in the NS5-brane …
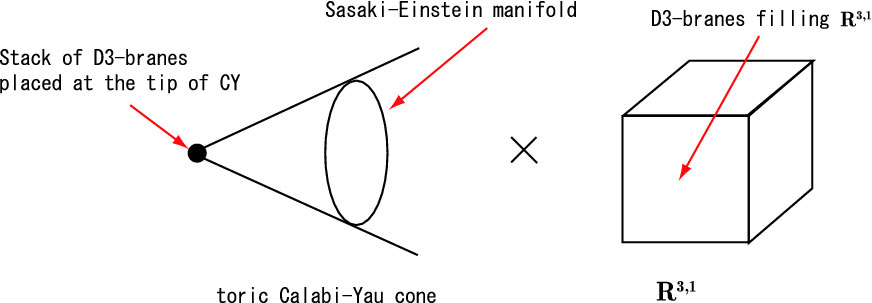
D3-Branes, Second Quantization, Sasaki–Einstein Manifolds And Calabi–Yau ‘Tips’
In my last post, I introduced the notions of …
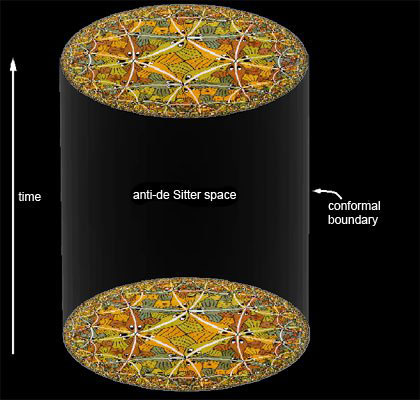
The Riemann-Lebesgue Lemma, D=11/ D=10 SuperGravity Actions, and Fourier Analysis
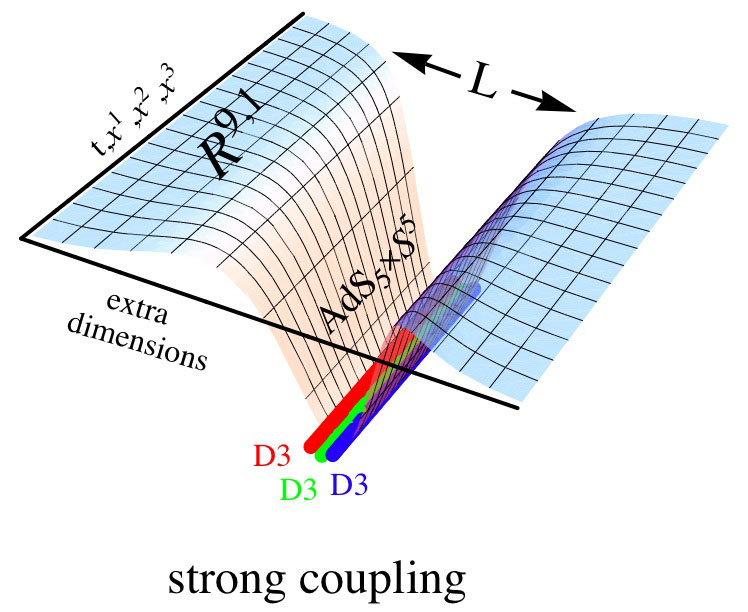
In my last post, I used the GKP-Witten relation…