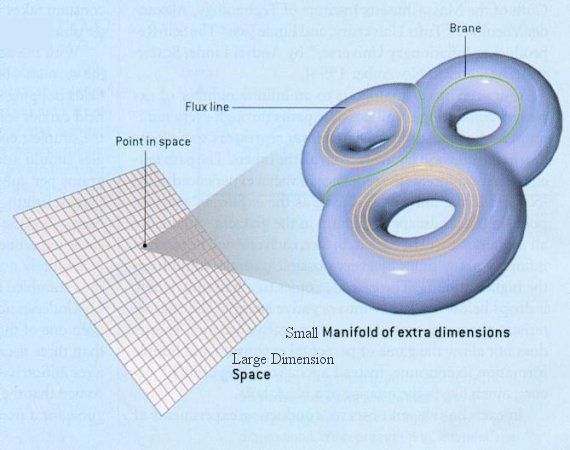
An equation means nothing to me unless it expresses a …
Kappa Symmetry, Dp-Brane Super-Lagrangian Action(s), and SuSy Calabi-Yau ‘Tipping’
If supersymmetry is to make touch with reality, not only …
A Sasaki-Einstein AdS/CFT Duality, SuSy, And Dp-Brane Conic Orbifolding Of GR
The main appeal of the AdS/CFT duality is its holographic…
A Dp–Dq Brane SuSy Dirac-Born–Infeld Derivation Of Quantum Cosmological Inflation
Although the standard received view of inflationary cosmology does explain…