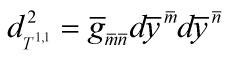For a full mathematical definition of ‘orbifold’ summarized above, check …
Universal Kähler Modulus and Randall-Sundrum 5D Brane Action
Continuing, we last saw that the corresponding nonlinear sigma model…
Klebanov-Strassler Warped Conifold Analysis, Calabi-Yau 3-Fold and AdS/CFT Duality
This is deep, and in this post, I will …