One of the deepest result in quantum physics is that …
String-Theory and Calabi-Yau Fourfolding of M-Theory
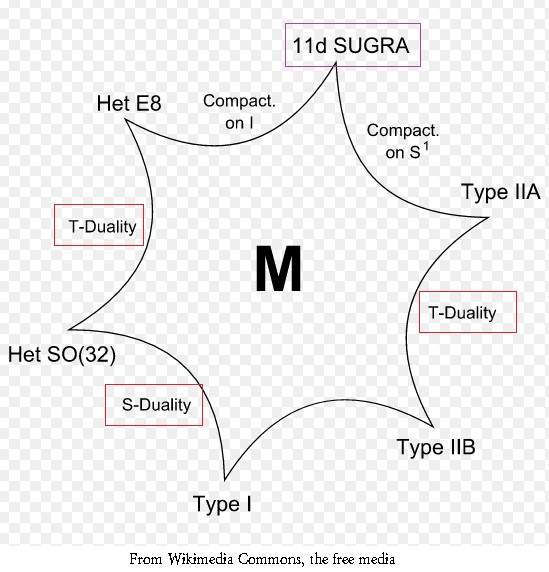
In this post, I will carry a Calabi-Yau fourfold compactification …
Realizing Quantum NonLocality in SuperString/M-Theory
Here I shall discuss perhaps the deepest aspect and advantage …