Nature is a mutable cloud, which is always and never the same. ~ Ralph Waldo Emerson!
Where there is life there is a pattern, and where there is a pattern there is mathematics. Once that germ of rationality and order exists to turn a chaos into a cosmos, then so does mathematics. There could not be a non-mathematical Universe containing living observers.
John D. Barrow, The Artful Universe (1995)
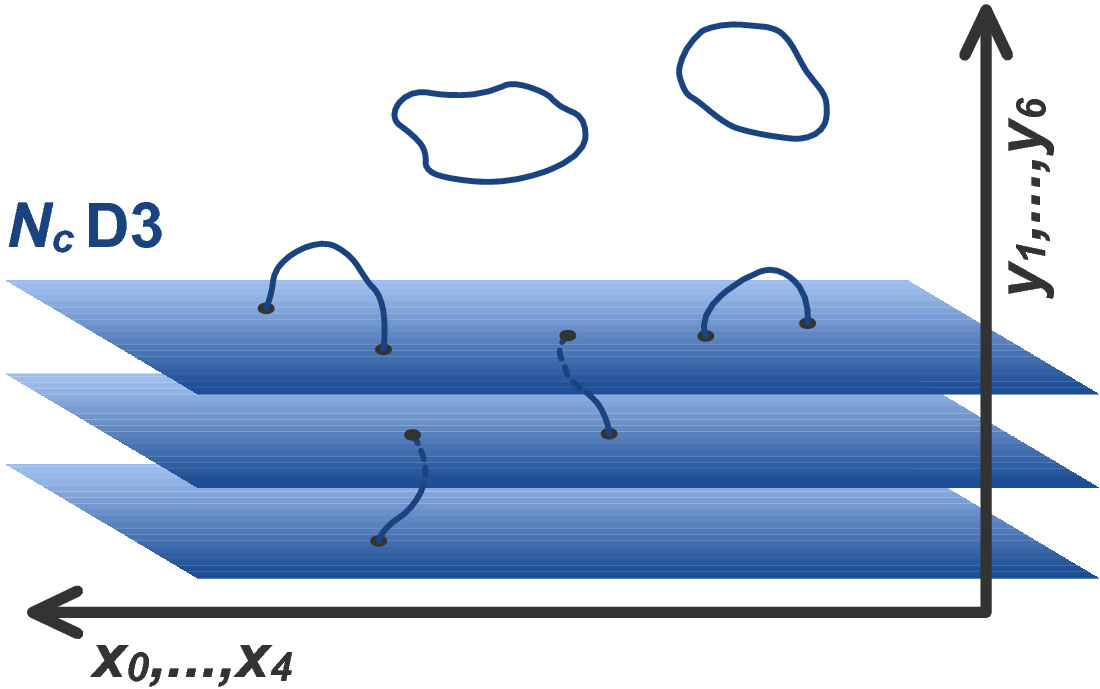
I last derived the D3-brane effective action in the NS5-brane geometry, via the D3-brane self-duality and Poincaré invariance properties as such:
![]()
with
![]()
![]() being the D3-brane tension, and
being the D3-brane tension, and ![]() ,
, ![]() are the RR-4 and RR-2 exterior forms. In order for the effective action to be integrable with fields in 2nd-quantized form, one must work under the Gaillard-Zumino Condition: that is – using 8-loop counterterms with superspace torsion
are the RR-4 and RR-2 exterior forms. In order for the effective action to be integrable with fields in 2nd-quantized form, one must work under the Gaillard-Zumino Condition: that is – using 8-loop counterterms with superspace torsion
![]()
where ![]() is the superfield torsion. One starts with a Lagrangian
is the superfield torsion. One starts with a Lagrangian
![]()
in D = 4, with a dependence on a ![]() gauge field strength
gauge field strength ![]() , metric
, metric ![]() , and matter field
, and matter field ![]() : so, we now have
: so, we now have
![]() ,
, ![]() and the Hodge dual components for the tensor
and the Hodge dual components for the tensor ![]() are given by
are given by
![]()
![]()
The Gaillard-Zumino Condition now is fundamentally an infinitesimal duality transformation of ![]() and
and ![]() and matter transformation given by
and matter transformation given by
![]()
![]()
![]()
Now, the Lagrangian must transform as
![]()
and one has a ![]() transformation given by
transformation given by ![]() ,
, ![]() , and so the Lagrangian is given by
, and so the Lagrangian is given by
![]()
and by D3-brane self-duality, it follows that
![]()
Now we are in a position to analyse the D3-brane action, and for simplicity but with no loss of information, without scalar supergravity backgrounds. Let ![]() be a bosonic brane coordinatization in D = 10 flat target bulk space
be a bosonic brane coordinatization in D = 10 flat target bulk space ![]() and
and ![]() its fermionic partner given by the Majorana-Weyl spinor index
its fermionic partner given by the Majorana-Weyl spinor index ![]() with N = 2 SuSy index
with N = 2 SuSy index ![]() . The D3 action for the brane coordinates
. The D3 action for the brane coordinates ![]() and worldvolume gauge field
and worldvolume gauge field ![]() must have Kappa symmetry and we require N = 2 SuSy: So,
must have Kappa symmetry and we require N = 2 SuSy: So,
![]()
where
![]()
![Rendered by QuickLaTeX.com \[{G_{\mu \nu }} = \prod _\mu ^M{\prod _{\nu M}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d2f55c6356f804ae55806ccdff4ade56_l3.png)
![]()
![]()
with ![]() being the Pauli matrices and act on the N = 2 SuSy indices. The 1-form defined by
being the Pauli matrices and act on the N = 2 SuSy indices. The 1-form defined by
![Rendered by QuickLaTeX.com \[\prod _\mu ^M \equiv d{x^M} + \overline {\theta \,} {\Gamma ^M}d\theta \equiv d{\sigma ^\mu }\prod _\mu ^M\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-47f8a8bfe1caf94d5e3ca50b685f4a66_l3.png)
and
![Rendered by QuickLaTeX.com \[\prod _\mu ^M = {\partial _\mu }{\chi ^{{M^\mu }}} - \overline \theta \,{\Gamma ^M}{\partial _\mu }d\theta = d{\chi ^M} + \frac{1}{2}\overline \theta \,{\Gamma ^M}d\theta \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-34f65aedaf54e9394e14b281fb6fc286_l3.png)
By use of exterior differential forms on the bulk, with an RR pull-back 2-form ![]() and 4-form
and 4-form ![]() , we get
, we get
![]()
![]()
and
![]()
and ![]() is given by
is given by
![Rendered by QuickLaTeX.com \[\begin{array}{c}\Xi = \frac{1}{6}\overline \theta {{\not \prod }^3}{\tau _3}\,{\tau _1}\,d\theta - \frac{1}{{12}}\overline \theta \left( {{{\not \prod }^2}{{\not \beta }_0} + \not \prod {\beta _0}\not \prod + {{\not \beta }_0}{{\not \prod }^2}} \right){\tau _3}\,{\tau _1}\,d\theta \\ + \frac{1}{{18}}\overline \theta \left( {\not \prod \not \beta _0^2 + {{\not \beta }_0}\not \prod } \right)\tau {\,_3}{\tau _1}\,d\theta - \frac{1}{{12}}\overline \theta \not \prod {\tau _{\left[ {1,d\theta \overline {\theta \,{{\not \beta }_{0{\tau _3}}}} } \right]}}\,d\theta \\ - \frac{1}{{24}}\overline \theta \not \beta _0^3\,{\tau _3}\,{\tau _1}\,d\theta \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-b1c42f772d634316515431c4537338d0_l3.png)
with ![]() . To check whether the Gaillard-Zumino Condition is met, we must calculate the first 2 terms of the condition:
. To check whether the Gaillard-Zumino Condition is met, we must calculate the first 2 terms of the condition:
so, ![]() is given by
is given by
![]()
where I have made an explicit use of the determinant formula for the four-by-four matrix
![]()
![]()
and by the Hodge duality, ![]() can be derived as
can be derived as
![]()
and by the GKP-Witten relation for the D3-brane action
![]()
one gets
![]()
and by conjugation, one derives the essential identity
![]()
A few remarks are in order now on the bosonic truncation of the D3-brane action. Note in the above equation, the right-hand-side vanishes completely, and so the Lagrangian transforms accordingly as
![]()
The supersymmetry situation under the Gaillard-Zumino Condition can now be considered for the matter field contributions. For a D3-brane, the matter fields transform as
![]()
![]()
and hence we get
![]()
![]()
![]()
while noting that the Majorana-Weyl fermions: ![]() and
and ![]() transform as
transform as ![]() group doublet and the gauge variation of the total Lagrangian with respect to matter fields transforms as
group doublet and the gauge variation of the total Lagrangian with respect to matter fields transforms as
![]()
where ![]() is the Hodge dual of
is the Hodge dual of ![]() , with
, with
![]()
and the Poincaré invariance of D3-branes transfers to ![]() and induces a relation on the differential forms
and induces a relation on the differential forms
![]()
Combining the last 3 equations, we get
![]()
And so the D3-brane self-duality and Poincaré invariance are satisfied by the Gaillard-Zumino Condition. To second-quantize the D3-brane action, one must lift the ![]() duality by an introduction of a dilaton
duality by an introduction of a dilaton ![]() and axion
and axion ![]() living on constant background fields on the bulk space. The redefined Lagrangian, via D3-brane 4-dimensional worldvolume topological tori-throating becomes
living on constant background fields on the bulk space. The redefined Lagrangian, via D3-brane 4-dimensional worldvolume topological tori-throating becomes
![]()
and by such tori redefinition, we obtain
![]()
Next, I should work in the Hamiltonian framework to bring to light some deep issues in brane-dynamics.
Mathematics is not contained in its formulae, but ‘in’ the mental pauses the mathematician takes between thinking about them.