Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

How 4-D Physics Emerges from SuperString Theory Based on Exotic 4-D Manifolds

By Posted on In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Super String Theory, Supersymmetry, Witten Theory ,
photo

I last derived spacetime physics from the string worldsheet, here I shall derive 4-D physics on exotic manifolds in the context of super-string theory. Before proceeding, recall the key steps: since the solution to the Lagrange multiplier equation of motion is

    \[{v_b} = {\not \partial _b}\Psi _{scalar}^{{e^{H_{p + 1}^{{\rm{array}}}}}}\]

with its Clifford form

    \[\frac{{{{\not D}^{susy}}L}}{{\not \partial {{X'}^{25}}}} = i{\varepsilon ^{ab}}{\not \partial _a}{v_b} = 0\]

for {\Psi _{scalar}} any scalar. Hence, for {v_a}, we have:

    \[\frac{{\not D_\mu ^{susy}L}}{{{{\not \partial }_{{v_a}}}}} - {\mkern 1mu} \frac{\partial }{{{{\not \partial }_{{\sigma _b}}}}}\left( {\frac{{\not D_\nu ^{susy}L}}{{\not \partial \left( {{{\not \partial }_{b,{v_a}}}} \right)}}} \right) = 0 = {g^{ab}}\left[ {{G_{25,25,{v_a}}} + {G_{25,\mu }}{X^\mu }} \right] + i{\varepsilon ^{ab}}\left[ {{B_{25,\mu }}\not \partial {X^\mu } + {{\not \partial }_b}{X^{25}}} \right]\]

Now, by solving via a Dp \times Dp metric:

E_{\mu \nu }^m = {G_{\mu \nu }} + {B_{\mu \nu }}

we get the Dp action:

    \[S_p^D = \, - {T_p}\int\limits_{{\rm{worldvolumes}}} {{d^{p + 1}}} \xi \frac{{\not D_{\mu \nu }^{susy}L}}{{{{\not \partial }_{{v_a}}}}}{e^{ - {\Phi _{bos}}}}{\rm{de}}{{\rm{t}}^{1/2}}G_{ab}^{\exp \left( {H_{p + 1}^{{\rm{array}}}} \right)}\]

And since in 4-dimensional space-time, the mass of a Dp-brane can be derived as:

    \[{T_p}{e^{ - {\Phi _{bos}}}}\prod\limits_{i = 1}^p {\left( {2\pi nR} \right)} \]

by T-dualizing in the

    \[{X^p}\]

direction and factoring the dilaton, the dual is hence:

    \[\begin{array}{c}({T_p}\left( {2\pi \sqrt {\alpha '} } \right){e^{ - {\Phi _{bos}}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_p}} \right)} = \\{T_{p - 1}}{e^{ - \Phi _{bos}^{1/2}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_{p - 1}}} \right)} \end{array}\]

By matrix world-volume integral reduction on

    \[S_p^D = \, - {T_p}\int\limits_{{\rm{worldvolumes}}} {{d^{p + 1}}} \xi \frac{{\not D_{\mu \nu }^{susy}L}}{{{{\not \partial }_{{v_a}}}}}{e^{ - {\Phi _{bos}}}}{\rm{de}}{{\rm{t}}^{1/2}}G_{ab}^{\exp \left( {H_{p + 1}^{{\rm{array}}}} \right)}\]

the Polyakov action for the string is given as:

    \[{S^p} - \frac{1}{{4\pi \alpha '}}\int {{d^2}} \sigma \sqrt { - \gamma } {\gamma ^{ab}}{\not \partial _a}{X^\mu }{\not \partial _b}{X^\nu }{G_{\mu \nu }}\]

with {X^\mu }\left( {\tau ,\sigma } \right) the embedding of the string in target space, {\gamma _{ab}} the worldsheet metric, and {G_{\mu \nu }} the spacetime metric. The renormalization Lie-equation for the sigma-model on the string worldsheet entails that

    \[{\beta _{\mu \nu }} = \frac{{{\rm{d}}{G_{\mu \nu }}}}{{{\rm{dlog}}\Lambda }} = \alpha '{R_{\mu \nu }} + O\left( {{{\alpha '}^2}} \right) = 0\]

So, from

    \[\begin{array}{c}({T_p}\left( {2\pi \sqrt {\alpha '} } \right){e^{ - {\Phi _{bos}}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_p}} \right)} = \\{T_{p - 1}}{e^{ - \Phi _{bos}^{1/2}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_{p - 1}}} \right)} \end{array}\]

the Einstein vacuum field equation is hence encoded in the quantum structure of the conformal worldsheet theory as characterized by

    \[{\vartheta _\mu }\left( u \right){\vartheta _\nu }\left( v \right) = \lambda _{\mu \nu }^\rho \frac{{{\vartheta _\rho }}}{{{{\left( {u - v} \right)}^\# }}} + ...\]

Therefore, the β-function equation gives a definition of the stress-energy tensor for the worldsheet theory

    \[{\beta ^{\mu \nu }} = {T^{\mu \nu }} = \frac{{\delta \,{\Gamma _{eff}}}}{{\delta {G_{\mu \nu }}}}\]

with

    \[{e^{ - {\Gamma _{eff}}}} = \exp \left( {\int {{d^2}\sigma {G_{\mu \nu }}{T^{\mu \nu }}} } \right)\]

By holographic renormalization, it follows that the worldsheet quantum theory knows all about spacetime physics

as attested by

    \[\frac{d}{{{d_{{\sigma _p}}}}}\int\limits_{{\rm{worldvolumes}}}^p {{e^{H_{p + 1}^{{\rm{array}}}}}} + \underbrace {\sum\limits_{{\sigma _p}}^D {{{\left( {S_p^D} \right)}^{ - H_{p + 1}^{{\rm{array}}}}}} }_{{\rm{topologies}}}\]

The key to this post is the avoidance of the standard methods of deriving 4-D physics via compactification, flux stabilization, Dp-brane-theory or first-order AdS/CFT correspondence/holography and will attempt a purely geometric method based on exotic smooth 4-D topological manifolds.

To appreciate the uniqueness of 4-D manifolds, and why M-theory is essential for 4-D physics, absorb the following facts, from Alexandru Scorpan

 

postheaderp

 

and so, “there goes the neighborhood”: 

 

postheaderpp

 

This is where the magic of superstring theory comes in. When formulated on backgrounds containing 4-dimensional exotic {\mathbb{R}^4} rather than standard {\mathbb{R}^4}, topological surgical tensor-network methods allow 4-D exotic {\mathbb{R}^4} to orbifoldize with worldsheets of strings. So we re-capture the fact that in string theory, the notion of space-time as a smooth manifold is no longer valid due to vacuum fluctuations of the worldsheet, which is ‘complex’, where 4-D physics emerges as a classical-limit with a geometry (M, g, B), and such exotic {\mathbb{R}^4} relative to the background, are classified by the integral classes of {H^3}\left( {M,\mathbb{Z}} \right)-geometric objects representing the third cohomologies of the associated complex line bundles: hence the existence of Abelian gerbes, and the presence of B-field such that H is the curvature of such a gerbe means that the correct, semi-classical, geometry for string theory is the one based on Abelian gerbes supplementing Riemannian geometry and the dilaton is constant and F_{\mu \nu }^a vanishes, and the β-function forces the background be non-flat unless H = dB is zero.

Here’s a deep theorem proven by Torsten Asselmeyer-Maluga and Jerzy Król:

For any family of exotic {\mathbb{R}^4}‘s in the radial family whose members are embedded in standard {\mathbb{R}^4}, there exists an associated family of 3-spheres in the boundaries of the Akbulut-corks for these exotic {\mathbb{R}^4}’s and each such exotic 4-fold from that family is determined by the codimension-1 foliation of the corresponding 3-sphere, with non-vanishing Godbillon–Vey class in {H^3}\left( {{S^3},\mathbb{R}} \right). The radius in the family, \rho, and value of GV being related as GV = {\rho ^2}. Yet, the classification of D-branes in string backgrounds is characterized by K-theory of the background.

Here is where M-theory comes in. Without loss of generality, we can take the bosonic SU{\left( 2 \right)_k}-WZW model. Now, as k \to \infty, D-branes in SU\left( 2 \right) G-manifolds are determined by wrapping the conjugacy classes of SU\left( 2 \right), and so there are k + 1 D-branes on the level k SU\left( 2 \right) WZW model. Non-commutative gauge theory emerges on the tangent bundle of the monster group-manifold. Now, let J be the representation of SU{\left( 2 \right)_k}.

So, the non-commutative action for the dynamics of N-branes of type J in the string regime is hence:

 

eq1

 

with the curvature form:

    \[\begin{array}{c}{F_{\mu \nu }}\left( A \right) = i{L_\mu }{A_\nu } - i{L_\nu }{A_\mu } + i\left[ {{A_\mu },{A_\nu }} \right]\\ + {f_{\mu \nu \rho }}{A^\rho }\end{array}\]

with the non-commutative Chern–Simons action being

    \[C{S_{\mu \nu \rho }}\left( A \right) = {L_\mu }{A_\nu }{A_\rho } + \frac{1}{3}{A_\mu }\left[ {{A_\nu },{A_\rho }} \right]\]

The uniqueness of superstring theory is that the fields 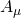{A_\mu }, µ = 1, 2, 3, are defined on a fuzzy 2-sphere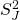 S_J^2

that is:

    \[{A_\mu } = \sum\nolimits_{j,a} {a_{j,a}^\mu } Y_a^j\]

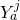with Y_a^j the fuzzy spherical string-harmonics and 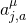a_{j,a}^\mu the Chan–Paton matrix-valued coefficients

Thus, the equations of motion are:

    \[{L_\mu }{F^{\mu \nu }} + \left[ {{A_\mu },{F^{\mu \nu }}} \right] = 0\]

whose solutions describe the dynamics of the brane, and so there exists a continuous map between the partition functions governed by the Verlinde fusion rules coefficients

    \[N_{{J_{Nj}}}^l\]

which is

    \[N{\chi _j}\left( q \right)\]

and the sum of characters

    \[\sum\nolimits_j {N_{{J_{Nj}}}^l} \chi l\left( q \right)\]

where

    \[N = 2{J_N} + 1\]

Therefore, there are k + 1 stable branes wrapping the conjugacy classes indexed by J and so putting N point-like branes at the pole causes their decay to the spherical brane {J_N} wrapping the conjugacy class. Adding more point-like branes to the stack at the pole gives the more distant {S^2} branes until one reaches the opposite pole.

In the case of SU\left( 2 \right), one gets:

    \[K_H^ * \left( {{S^3}} \right) = {\mathbb{Z}_K}\]

So, by the above theorem, we can place SU\left( 2 \right) at the boundary of the Akbulut-cork for some exotic smooth \mathbb{R}_k^4 from the radial family.

Deep: it follows that small exotic {\mathbb{R}^4}’s generate the group of Ramond-Ramond charges of D-branes in the curved background of

    \[{S^3} \subset {\mathbb{R}^4}\]

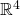So we have: the classification of Ramond-Ramond charges of the branes on the background given by the group manifold SU\left( 2 \right) at the level k corresponds to the exotic smoothness on {\mathbb{R}^4} containing 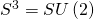{S^3} = SU\left( 2 \right) as the part of the boundary of the Akbulut-cork, and the geometry of the stack of NS5-branes in type II superstring theories correlates with the change of the smoothness structure on the transversal 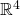{\mathbb{R}^4} that induces a Chan–Paton Hilbert space, and so topological quantum Dp-branes are exactly those branes determined by the wild embeddings 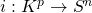i:{K^p} \to {S^n}. Hence, 4-D physics arises in the regime of SUGRA backreactions

as witnessed by:

 

eq12

 

Thus, exotic 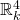\mathbb{R}_k^4 regions in 4-space-time act as magnetic monopoles! And in Riemannian geometry and General Relativity, there is always some large exotic smooth 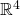{\mathbb{R}^4} that acts as an external source of gravitational fields in 4-D space-time

 

Untitled

 

previously

How the String Theory Worldsheet 'Knows' All About Spacetime Physics

up next

Realizing Quantum NonLocality in SuperString/M-Theory
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on
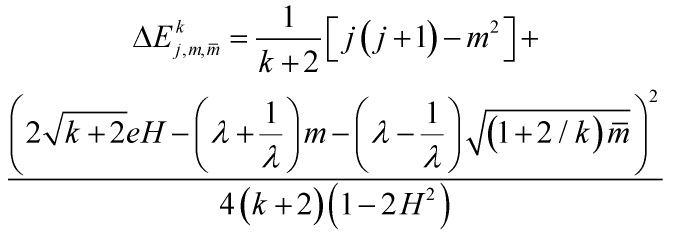
1 Response
  • String-Theory and the String/Non-Local-'Particles' Duality
    Tuesday, July 26, 2016

    […] 'non-local-particles' (Pages 51-67) can be symmetrically identified with strings in string-theory. Consider, as I showed, the non-commutative action for the dynamics of N-branes of type J in the string […]