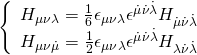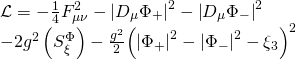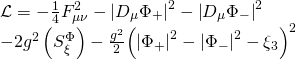In this, part III, of our series of deriving the Standard ΛCDM Model of cosmology from Type-IIB SUGRA by an identification of the inflaton with the Gukov-Vafa-Witten topologically twisted Kähler modulus, we recall that in part two, we derived the action of the ![]() and the
and the ![]() branes of our system. To complete the derivation, we need the
branes of our system. To complete the derivation, we need the ![]() -term, and to obtain it, we need an embedding in M-theory. Let us derive the
-term, and to obtain it, we need an embedding in M-theory. Let us derive the ![]() action in a curved background given by our metric. The effective action is given by:
action in a curved background given by our metric. The effective action is given by:
![]()
has a Kaloper-Sorbo reduction to:
![]()
with:
![]()
![]()
![]()
![]()
where we have integrated out the ![]() fluctuation-modes in the
fluctuation-modes in the ![]() directions. The
directions. The ![]() brane covariant 2-form is composed of two terms:
brane covariant 2-form is composed of two terms:
![]()
with ![]() the field strength of the vector field
the field strength of the vector field ![]() living on the brane and
living on the brane and ![]() the pullback of the space-time NS-NS two-form field to the worldvolume of the
the pullback of the space-time NS-NS two-form field to the worldvolume of the ![]() -brane, with a Chern-Simons part induced by the RR field. With:
-brane, with a Chern-Simons part induced by the RR field. With:
![]()
the volume of a fixed ![]() , then integrating over
, then integrating over ![]() gives us:
gives us:
![]()
with:
![]()
![]()
![]()
![]()
![]()
and with coupling constants:
![]()
with our four-form given by:
![]()
Thus the ![]() -Chern-Simons term becomes:
-Chern-Simons term becomes:
![]()
with:
![]()
Now since the ![]() invariant 5-form is self-dual in 10-D, there must be a 4-form field in all 10-dimensions. Hence, our action becomes:
invariant 5-form is self-dual in 10-D, there must be a 4-form field in all 10-dimensions. Hence, our action becomes:
![]()
with:
![]()
![]()
![]()
![]()
Adding coincident ![]() -branes forces us to generalize the connection
-branes forces us to generalize the connection ![]() with corresponding Chan-Patton
with corresponding Chan-Patton ![]() gauge fields and a Yukawa quiver gauge-theory describing the system.
gauge fields and a Yukawa quiver gauge-theory describing the system.
After embedding the ![]() -brane in the same metric and Ramond-Ramond system, we get the following
-brane in the same metric and Ramond-Ramond system, we get the following ![]() -action:
-action:
![]()
with:
![]()
![]()
![]()
Hence, the ![]() -modified total action is:
-modified total action is:
![]()
with:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
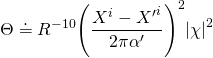
![]()
Note that the hypermultiplet covariant derivative is still of the form:
![]()
hence, we can do the following gauge transformations:
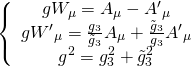
consistent with:
![]()
Thus, our action now has the form:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=\int{{{{d}^{4}}}}x\sqrt{{-{{g}_{E}}}}\left[ {-\frac{1}{4}} \right.{{\left( {{{F}_{W}}} \right)}^{2}}-\frac{1}{4}{{\left( {{{F}_{{{W}'}}}} \right)}^{2}}-\\{{\left| {\partial S} \right|}^{2}}-{{\left| {\partial {S}'} \right|}^{2}}-{{R}^{{-12}}}\frac{1}{{8g_{7}^{2}}}\int_{{K3}}{{{{{\tilde{F}}}^{D}}^{-}\wedge *{{{\tilde{F}}}^{D}}^{-}}}-\\{{\left| {{{D}_{\mu }}\chi } \right|}^{2}}-2{{g}^{2}}{{\left| S \right|}^{2}}{{\left| \chi \right|}^{2}}\left. {-\frac{{\left( {g_{3}^{2}+\tilde{g}_{3}^{2}} \right)}}{2}{{{\left( {{{\chi }^{\dagger }}{{\sigma }^{A}}\chi } \right)}}^{2}}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-daa9b8f3bdc50e63050642e211f74c8f_l3.png)
Our string sectors and all our fields satisfy the required N = 1 chiral superfield-normalization condition and we have rigid N = 2 supersymmetry that gets naturally broken to N = 1 when coupled to gravity in D = 4. Now we need an embedding in M-theory in order to derive our ![]() -term. Take M-theory with
-term. Take M-theory with ![]() parallel
parallel ![]() branes spread along the orbifold
branes spread along the orbifold ![]() , which preserves
, which preserves ![]() SUSY in 4-D, with the wrapped 6-D background along
SUSY in 4-D, with the wrapped 6-D background along ![]() . Each
. Each ![]() brane fills the 4-D non-compact spacetime and wraps the same holomorphic two-cycles
brane fills the 4-D non-compact spacetime and wraps the same holomorphic two-cycles ![]() on the Calabi-Yau. The main terms of the 4-D
on the Calabi-Yau. The main terms of the 4-D ![]() SYM theory are the volume modulus of the Calabi-Yau:
SYM theory are the volume modulus of the Calabi-Yau:


![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{\mathcal{L}}^{Q}}=-\frac{1}{2}\left[ {{{{\left( {{{\partial }_{\mu }}{{X}^{i}}} \right)}}^{2}}+{{{\left( {{{\partial }_{{\dot{\mu }}}}{{X}^{i}}} \right)}}^{2}}} \right]+\\\frac{i}{2}\left\langle {\bar{\Psi },\left( {{{\Gamma }^{\mu }}{{\partial }_{\mu }}+{{\Gamma }^{{\dot{\mu }}}}{{\partial }_{{\dot{\mu }}}}} \right)\Psi } \right\rangle -\\\frac{1}{4}{{F}_{{\mu \dot{\nu }\dot{\lambda }}}}^{2}-\frac{1}{{12}}{{F}_{{\dot{\mu }\dot{\nu }\dot{\lambda }}}}^{2}-\frac{1}{2}{{\epsilon }^{{\mu \nu \lambda }}}{{\epsilon }^{{\dot{\mu }\dot{\nu }\dot{\lambda }}}}{{\partial }_{\mu }}{{A}_{{\nu \dot{\mu }}}}{{\partial }_{{\dot{\nu }}}}{{A}_{{\lambda \dot{\lambda }}}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2e60523929b3692855ecff6f9f61ea1a_l3.png)