Quantum Geometry, Emergence and Noncommutative Spacetime

By George Shiber Friday, August 5, 2016Saturday, August 17, 2019 In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Super String Theory Non-Commutative Spacetime, Quantum Geometry

I will show that any field theory that supervenes on noncommutative spacetime analytically leads to a quantum geometry embedding quantum gravity, and leads to an interpretation of classical Einsteinian spacetime and quantum gravity as emergent properties of symplectic noncommutative spacetime. Again, two good references are my last post and P. Aschieri.

I will start with matrix models, where T-duality reflects a change of dimensionality, given by:

$i{\not D_\mu } = i{\not \partial _\mu } + {A_\mu } \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} {\Phi ^a}$

and applied to the $U\left( {N \to \infty } \right)$ Yang-Mills theory in d-dimensions:

$\begin{array}{l}{S_M} = - \frac{1}{{{G_s}}}\int {{d^d}} \tilde z\,{\rm{Tr}}\left( {\frac{1}{4}} \right.{F_{\mu \nu }}{F^{\mu \nu }} + \\\frac{1}{2}{{\not D}_\mu }{\Phi ^a}{{\not D}^\mu }{\Phi ^a} - \left. {\frac{1}{4}{{\left[ {{\Phi ^a},{\Phi ^b}} \right]}^2}} \right)\end{array}$

we get the n-dimensional IKKT matrix model, in generic form:

${S_{IKKT}} = - \frac{{2\pi }}{{{g_s}{\kappa ^2}}}{\rm{Tr}}\left( {\frac{1}{4}\left[ {{X^M},{X^N}} \right]\left[ {{X_M},{X_N}} \right]} \right)$

and the n-dimensional BFSS matrix model in the case of the Lorentzian signature:

${S_{BFSS}} = - \frac{1}{{{G_s}}}\int {dt} {\rm{Tr}}\left( {\frac{1}{2}{{\not D}_n}{\Phi ^a}{{\not D}^n}{\Phi ^a} - \frac{1}{4}{{\left[ {{\Phi ^a},{\Phi ^b}} \right]}^{n + 2}}} \right)$

both of which, given the Morita-reduction to quantum mechanics, reflects the latter’s noncommutative phase space:

$\left[ {{x^a},{p_b}} \right] = i\hbar {\delta ^a}_b$

leading to the Heisenberg’s uncertainty relation, and the large energy localization at Planck distances deform the background geometry according to the equivalence principle. This kind of backreaction of the background spacetime introduces a new kind of spacetime-uncertainties that reflect noncommutative spacetime,

thus, at Planck distances and ‘scales’, quantum mechanics necessarily implies noncommutative geometry

with space $M$ derived from a symplectic structure

${B^s} = \frac{1}{2}{B^s}_{ab}d{y^a} \wedge d{y^b}$

one then quantizes the spacetime via its quantum-phase Poisson algebraic structure:

${\theta ^{ab}} \equiv {\left( {{B^{ - 1}}} \right)^{ab}}$

hence, we have, for: $f,g \in {\mathbb{C}^\infty }\left( M \right)$

$\begin{array}{c}\left\{ {f,g} \right\} = {\theta ^{ab}}\left( {\frac{{\not \partial f}}{{\not \partial {y^a}}}\frac{{\not \partial g}}{{\not \partial {y^b}}} - \frac{{\not \partial f}}{{\not \partial {y^b}}}\frac{{\not \partial g}}{{\not \partial {y^a}}}} \right)\\ \Rightarrow - i\left[ {\hat f,\hat g} \right]\end{array}$

Thus, the noncommutative algebra of operators is isomorphic to the deformed algebra of functions defined by the Weyl-Moyal product:

$\begin{array}{l}\left\{ {f,g} \right\} \cong \left( {f{ * _{wm}}g} \right)\left( y \right) = \\\exp \left( {\frac{i}{2}{\theta ^{ab}}\not \partial _a^y\not \partial _b^z} \right)f\left( y \right)g\left( z \right)\left| {_{y = z}} \right.\end{array}$

I can define now a noncommutative space ${\mathbb{R}^{2n}}$ via the commutation relation:

${\left[ {{y^a},{y^b}} \right]_{{ * _{wm}}}} = i{\theta ^{ab}}$

which allows us to interpret it as a noncommutative phase-space with Poisson structure given by ${\theta ^{ab}}$ .

Any field $\hat \phi \in {{\rm A}_\theta }$ can be expanded in terms of the complete-operator-basis:

$\left\{ {\begin{array}{*{20}{c}}{{{\rm A}_\theta } = \left\{ {\left| m \right\rangle \left\langle n \right|,n,m = 0,...} \right\}}\\{\hat \phi \left( {x,y} \right)\sum\limits_{n,m} {{M_{mn}}\left| m \right\rangle \left\langle n \right|} }\end{array}} \right.$

with ${{\rm A}_\theta }$ a C*-algebra, that is:

${e^{ik \cdot y}}{ * _{wm}}f\left( y \right){ * _{wm}}{e^{ - ik \cdot y}} = f\left( {y + \theta \cdot k} \right)$

in infinitesimal form:

${\left[ {{y^a},f} \right]_{{ * _{wm}}}} = i{\theta ^{ab}}{\not \partial _b}f$

The coordinates ${y^a}$ in a gauge-theoretic setting will get promoted to the covariant coordinates defined by:

${x^a}\left( y \right) \equiv {y^a} + {\theta ^{ab}}{\hat A_b}\left( y \right)$

and

${\left[ {{y^a},f} \right]_{{ * _{wm}}}} = i{\theta ^{ab}}{\not \partial _b}f$

get covariantized as:

and from

${\theta ^{ab}} \equiv {\left( {{B^{ - 1}}} \right)^{ab}}$

one gets a quantum geometry relation:

${V_a}\left( y \right) \equiv V_a^\alpha \left( y \right){\not \partial _\alpha }$

constituting an orthonormal frame and defining vielbeins of a gravitational metric.

Quantum geometry, gravity and the Dirac-Born-Infeld action

To interpret emergent gravity, qua ‘theory’ in quantum geometry, up to isomorphism, note that I must identify the diffeomorphism-symmetry, which forms the underlying local symmetry of gravity. That is mathematically straightforward, since emergent gravity is rooted in symplectic geometry:

Darboux’s theorem in symplectic geometry is equivalent to the equivalence-principle in general relativity

DT says basically that for:

$\left[ {\omega '} \right] = \left[ \omega \right] \in {H^2}\left( M \right)$

with

$\omega ' = \omega + dA$

the following is true:

$\exists \phi :M \to M \in diff\left( M \right)$

such that:

$\frac{{\not \partial {x^\alpha }}}{{\not \partial {y^a}}}\frac{{\not \partial {x^\beta }}}{{\not \partial {y^b}}}{\omega '_{\alpha \beta }}\left( x \right) = {\omega _{ab}}\left( y \right)$

Thus, the local equivalence between symplectic structures leads to an amazing identity between Dirac-Born-Infeld actions:

$\begin{array}{l}\int_{dbi} {{d^{p + 1}}} x\sqrt {\det \left( {g + \kappa \left( {{B^s} + F\left( x \right)} \right)} \right)} \\ = \int_{dbi} {{d^{p + 1}}} y\sqrt {\det \left( {\kappa {B^s} + h\left( y \right)} \right)} \end{array}$

with the metaplectic fluctuations of gauge fields appearing as an induced metric on the brane given by:

${h_{ab}}^\prime \left( y \right) = \frac{{\not \partial {x^\alpha }}}{{\not \partial {y^a}}}\frac{{\not \partial {x^\beta }}}{{\not \partial {y^b}}}{g_{\alpha \beta }}$

Now, I can consider the D-branes data: the triple $\left( {M,g,{B^s}} \right)$ , $M$ a smooth manifold equipped with a metric $g$ and a symplectic structure ${B^s}$ . The above Dirac-Born-Infeld action guarantees that:

$\left( {M,g,{B^s}} \right) = \left( {M,g + \kappa {B^s}} \right)$

Thus, the induced D-manifold defined by the metaplectic generalized quantum geometry continuously interpolates between a symplectic geometry $\left( {\left| {\kappa {B^s}{g^{ - 1}}} \right| \gg 1} \right)$ and a Riemannian geometry $\left( {\left| {\kappa {B^s}{g^{ - 1}}} \right| \ll 1} \right)$

and so, the dynamical fields in

$\int_{dbi} {{d^{p + 1}}} x\sqrt {\det \left( {g + \kappa \left( {{B^s} + F\left( x \right)} \right)} \right)}$

act as deformation of the symplectic structure:

$\Omega \left( x \right) = {B^s} + F\left( x \right)$

in $\left( {M,J,\Omega } \right)$

and those in

$= \int_{dbi} {{d^{p + 1}}} y\sqrt {\det \left( {\kappa {B^s} + h\left( y \right)} \right)}$

deform the complex structure

$J'\left( y \right) \in \left( {M',J',{B^s}} \right)$

via the metric

${h_{ab}}^\prime \left( y \right) = \frac{{\not \partial {x^\alpha }}}{{\not \partial {y^a}}}\frac{{\not \partial {x^\beta }}}{{\not \partial {y^b}}}{g_{\alpha \beta }}$

Thus the isomorphism:

$\left( {M,J,\Omega } \right) \cong \left( {M',J',{B^s}} \right)$

reflecting homological mirror symmetry!

Quantum geometry and emergent gravity from noncommutative field theory

The above correspondence between noncommutative field theory and gravity can now be mathematically fleshed out via the self-dual sectors of noncommutative gauge theories.

Take a noncommutative $U(1)$ gauge theory on

${{\rm{R}}^D} = \mathbb{R}_C^d \times \mathbb{R}_{NC}^{2n}$

and decompose D-dimensional gauge fields as:

${A_M}\left( {z,y} \right) = \left( {{A_\mu },{\Phi ^a}} \right)\left( {z,y} \right)$

with

${\Phi ^a}\left( {z,y} \right) \equiv {x^a}\left( {z,y} \right)/\kappa$

adjoint Higgs fields defined by the covariant coordinates

${x^a}\left( y \right) \equiv {y^a} + {\theta ^{ab}}{\hat A_b}\left( y \right)$

Then, the matrix representation

allows us to identify the noncommutative 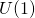$U(1)$ gauge theory on 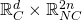$\mathbb{R}_C^d \times \mathbb{R}_{NC}^{2n}$ with the 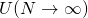$U(N \to \infty )$ Yang-Mills theory on D-dimensional commutative space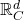 $\mathbb{R}_C^d$

So, given:

D-dimensional noncommutative $U(1)$ gauge fields

${A_M}\left( {z,y} \right) = \left( {{A_\mu },{\Phi ^a}} \right)\left( {z,y} \right)$

can be interpreted as gauge fields on $\mathbb{R}_C^d$ taking values in the Lie algebra of volume-preserving vector fields on a 2n-dimensional gauge-group-manifold

$G = SDiff\left( X \right)$

as:

${A_\mu }\left( z \right) = A_\mu ^a\left( {z,y} \right)\frac{{\not \partial }}{{\not \partial {y^a}}}$

with:

${\Phi _a}\left( z \right) = \Phi _a^b\left( {z,y} \right)\frac{{\not \partial }}{{\not \partial {y^b}}}$

Now, since

$\left\{ {\begin{array}{*{20}{c}}{{f^{ - 1}}\left( {{{\not D}_1},...,{{\not D}_d},{\Phi _1},...,{\Phi _{2n}}} \right)}\\{{{\not D}_\mu } \equiv {{\not \partial }_\mu } - i{A_\mu }\left( z \right)}\end{array}} \right.$

forms an orthonormal frame and therefore defines a metric on

${\rm{R}}_C^d \times X$

with volume form:

$\upsilon = {d^d}z \wedge \omega$

with $f$ a scalar, defined by:

${f^2}: = \omega \left( {{\Phi _1},...,{\Phi _{2n}}} \right)$

such that:

$\begin{array}{c}d{s^2} = {f^2}{\eta _{\mu \nu }}d{z^\nu } + \\{f^2}{\delta _{ab}}V_c^aV_d^b\left( {d{y^c} - {\rm A}_\theta ^c} \right)\left( {d{y^d} - {\rm A}_\theta ^d} \right)\end{array}$

We have then that

gravity does emerge from the Picard-metaplectic-pull-back on the cohomological algebra corresponding to the quantum geometry

described above, and the deep part is obvious:

an emergent gravity from noncommutative field theories entails gravity is not a fundamental force in nature and analytically avoids the problems plaguing quantum-gravity theories, most seriously, the problem of renormalization-group-finiteness. Thus, corollary: spacetime as well as Lorentz symmetry are emergent from gauge field interactions, and at the Planck-scale, spacetime exhibits dimensional reduction, raising the philosophical question as to how and why is spacetime 4-D at the classical Einsteinian ‘level’

Deep clue:

comparing polarizations of photons and gravitons in D-dimensions:

the following cannot be a miraculous coincidence or cosmic accident:

$\begin{array}{c}{A_\mu } = D - 2 = \frac{{D\left( {D - 3} \right)}}{2} = {g_{\mu \nu }}\\ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{D = 1}\\{D = 4}\end{array}} \right.\end{array}$

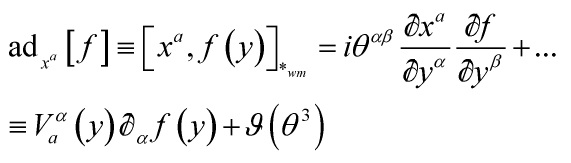
1 Response

4-D Effective String-Theory and No-Singularity Cosmology
Monday, August 8, 2016

[…] and analogously with quantum gravity theories must presuppose non-commutative spacetime and quantum geometry, consistency requirements on same said theories indicate no-singularity cosmology scenarios: this […]

Quantum Geometry, Emergence and Noncommutative Spacetime

thus, at Planck distances and ‘scales’, quantum mechanics necessarily implies noncommutative geometry

Quantum geometry, gravity and the Dirac-Born-Infeld action

Darboux’s theorem in symplectic geometry is equivalent to the equivalence-principle in general relativity