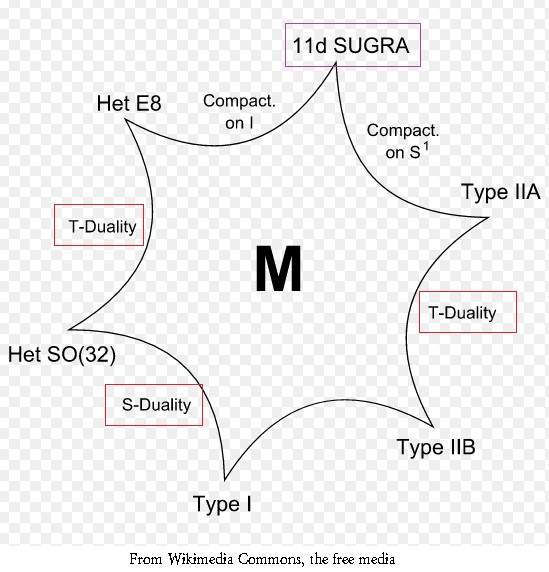
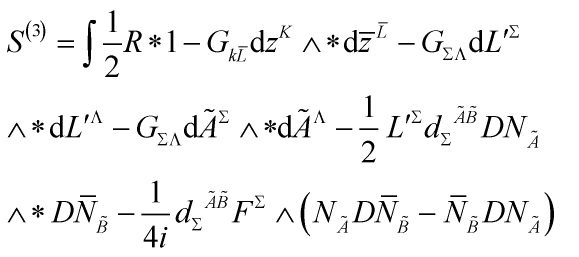In this post, I will carry a Calabi-Yau fourfold compactification of M-theory in a topologically smooth way. Since M-theory is the only quantum theory of gravity that provably has a finite renormalization group and is the only complete self-consistent GUT, such 4-D compactifications are essential in order to have a correspondence with 4-D spacetime. Recall I derived, via Clifford algebraic symmetry, the total action:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S^{Total}} = \frac{1}{{2\pi {\alpha ^\dagger }12}}\int\limits_{{\rm{world - volumes}}} {{d^{26}}} x\,d\,\Omega {\left( {{\phi _{INST}}} \right)^2}\sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} \,{e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}} \cdot \\\left( {{R_{icci}} - 4{{\left( {{{\not D}^{SuSy}}\left( {{\phi _{INST}}} \right)} \right)}^2}} \right) + \frac{1}{{12}}H_{3,\mu \nu \lambda }^bH_3^{b,\mu \nu \lambda }/A_\mu ^H + \sum\limits_{D - p - branes} {S_{Dp}^{WV}} \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ee1ece1964f54af749ce713bc472b175_l3.png)
which is deep since Clifford algebras are a quantization of exterior algebras, and applying to the ‘Einstein-Minkowski’ tangent bundle, we get via Gaussian matrix elimination, an expansion of ![]() via Green-functions, yielding M-Theory’s action:
via Green-functions, yielding M-Theory’s action:
![Rendered by QuickLaTeX.com \[{S_M} = \frac{1}{{{k^9}}}\int\limits_{{\rm{world - volumes}}} {{d^{11}}} \sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} {T_p}^{10}{\mkern 1mu} d{\mkern 1mu} \Omega {\left( {{\phi _{INST}}} \right)^{26}}\left( {{R_{icci}} - A_\mu ^H\frac{1}{{48}}G_4^2} \right) + \sum\limits_{Dp} {\not D_\mu ^{SuSy}} {e^{ - H_3^b}}/S_{Dp}^{WV} + \sum\limits_{Dp} {\not D_\nu ^{SuSy}} {e^{H_3^b}}/S_{Dp}^{SV}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-fad4e32f2dd760c5240235fd46ceb3d9_l3.png)
with ![]() the kappa symmetry gravitonic term and the supergravitational Hamiltonian term being:
the kappa symmetry gravitonic term and the supergravitational Hamiltonian term being:
![]()
Let  be a smooth Calabi-Yau fourfold and start with the bosonic 11-D SuGra sector
be a smooth Calabi-Yau fourfold and start with the bosonic 11-D SuGra sector
Start with the total M-theory action
Beginning with dimensional reduction of 11-D supergravity on ![]() , the bosonic part is given by:
, the bosonic part is given by:
![]()
with ![]() the 11-D Ricci scalar and
the 11-D Ricci scalar and ![]() the 4-form field strength for the 4-form
the 4-form field strength for the 4-form ![]() . Let
. Let ![]() be a metric on the Calabi-Yau 4-fold
be a metric on the Calabi-Yau 4-fold ![]() and pick the following backgrounds:
and pick the following backgrounds:
![]()
and
![]()
which ensure that the effective theory is a three-dimensional N = 2 supergravity one. Massless modes that arise from fluctuations of the metric are encoded by a Kähler form ![]() expanded as
expanded as
![]()
with ![]() the basis of harmonic two-forms and
the basis of harmonic two-forms and ![]() are 3-D scalar fields parametrizing the Kähler structure-deformations of
are 3-D scalar fields parametrizing the Kähler structure-deformations of ![]() .
.
Now, the massless modes that come from Heisenberg-fluctuations of M-theory’s three-form 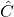 are
are
![]()
with
![]()
and ![]() a basis of harmonic (1, 2)-forms, with parametrization
a basis of harmonic (1, 2)-forms, with parametrization
![]()
with ![]() an integral-harmonic three-forms basis and
an integral-harmonic three-forms basis and ![]() holomorphic in complex structure.
holomorphic in complex structure.
Thus, we have
![Rendered by QuickLaTeX.com \[\begin{array}{l}\hat G = {\rm{d}}{A^\Sigma } \wedge {\omega _\Sigma } + D{N_{\tilde A}} \wedge {\Psi ^{\tilde A}} + \\D{{\bar N}_{\tilde A}} \wedge {{\bar \Psi }^{\tilde A}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-aecdbb8c99541fa0393df012198a7930_l3.png)
with the following holding:
![]()
and
![]()
Now, substituting the ansatz
![]()
and
![]()
into:
![]()
After a Weyl rescaling, thus bringing the effective action into Einstein-Sasaki frame, the 3-D effective theory is hence given by
The central mathematical entities in this expression, since I am working in M-theory, is the rescaled Kähler moduli
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{{L'}^{\,\Sigma }} = \frac{{{v^\Sigma }}}{{\tilde V}}}\\{\tilde V = \frac{1}{{4!}}\int_{{Y_4}} {{J^4}} }\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4a3408ae689a2c95a8378139886f0d12_l3.png)
with
![]()
and the following identity holding:
![]()
and expresses the intersection number of two-forms. Since the kinetic term for complex structure moduli ![]() depends on the Sasaki-Kähler metric:
depends on the Sasaki-Kähler metric:
![Rendered by QuickLaTeX.com \[{G_{K\bar L}} = - \frac{{\int_{{Y_4}} {\chi K \wedge \chi \bar L} }}{{\int_{{Y_4}} {\Omega \wedge \Omega } }} = - {\not \partial _z}k{\not \partial _{{{\bar z}^{\bar L}}}}\log \left( {\int_{{Y_4}} {\Omega \wedge \bar \Omega } } \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-465ffd33a081910dc9c82cff640e7c21_l3.png)
with ![]() a basis of harmonic (3, 1)-forms and
a basis of harmonic (3, 1)-forms and ![]() .
.
We can derive:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{G_{\Sigma \Lambda }} = \frac{{\bar V}}{4}\int_{{Y_4}} {{\omega _\Sigma }} \wedge * {\omega _\Lambda } = - \frac{1}{{8V}} \cdot \\\left( {{K_{\Sigma \Lambda }} - \frac{1}{{18V}}{K_\Sigma }{K_\Lambda }} \right)\\ = - \frac{1}{4}{{\not \partial }_{{{L'}^{\,\Sigma }}\,}}{{\not \partial }_{{{L'}^{\,\Lambda }}}}\log V\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-8efdf4d4199740b79654bf217788f7ce_l3.png)
with the definitions:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{K_\Sigma } = {K_{_{\Sigma \Lambda \Gamma \Delta }}}{{L'}^{\,\Lambda }}{{L'}^{\,\Gamma }}L'{\,^\Delta }}\\{{K_{_{\Sigma \Lambda }}} = {K_{_{\Sigma \Lambda \Gamma \Delta }}}{{L'}^{\,\Gamma }}L'{\,^\Delta }}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-b81aff31672dee09b1ead6f72730d0fb_l3.png)
and I explicitly used
![]()
and the couplings:
![]()
and
![]()
and made a green-functional use of
![]()
So we get then the following identities:
![]()
and
![]()
with complex and Kähler structure independent intersection numbers:
![]()
and
![]()
by solving
![]()
and via change-of-variables, substituting in
![Rendered by QuickLaTeX.com \[{S_M} = \frac{1}{{{k^9}}}\int\limits_{{\rm{world - volumes}}} {{d^{11}}} \sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} {T_p}^{10}{\mkern 1mu} d{\mkern 1mu} \Omega {\left( {{\phi _{INST}}} \right)^{26}}\left( {{R_{icci}} - A_\mu ^H\frac{1}{{48}}G_4^2} \right) + \sum\limits_{Dp} {\not D_\mu ^{SuSy}} {e^{ - H_3^b}}/S_{Dp}^{WV} + \sum\limits_{Dp} {\not D_\nu ^{SuSy}} {e^{H_3^b}}/S_{Dp}^{SV}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-fad4e32f2dd760c5240235fd46ceb3d9_l3.png)
one gets a solution to 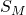 that dimensionally reduces to a Calabi-Yau hypersurface in weighted projective four-dimensional space, which is isomorphic to compactification on
that dimensionally reduces to a Calabi-Yau hypersurface in weighted projective four-dimensional space, which is isomorphic to compactification on