In this post, I shall analyze certain relations between holomorphic …
Probing Multi-Field Inflation with Supersymmetric Quantum Mechanics
Multi-scalar field cosmology is essential for solving the Wheeler-DeWitt equation…
Supersymmetric Group Field Cosmology and Loop Quantum Gravity
I showed that the curvature of the Ashtekar-Barbero connection of …
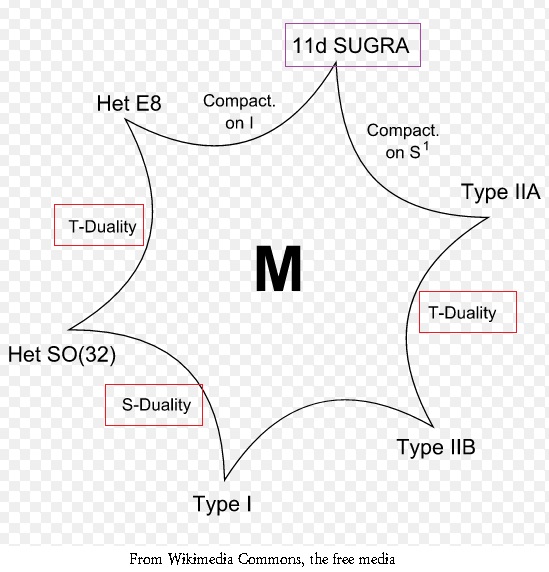
String-Theory and Calabi-Yau Fourfolding of M-Theory
In this post, I will carry a Calabi-Yau fourfold compactification …
Quantum Holomorphy, Kähler Manifolds and SuperString Theory
That the Poincaré supersymmetry is a phase of a deeper …