The Riemann-Lebesgue Lemma, D=11/ D=10 SuperGravity Actions, and Fourier Analysis

By George Shiber Friday, May 8, 2015Wednesday, September 4, 2019 In Grand Unification Physics, M Theory, Mathematical Physics, Philosophy Of Mathematics, Philosophy Of Physics, Philosophy Of Science, Super String Theory, Supersymmetry Heisenberg, infinity

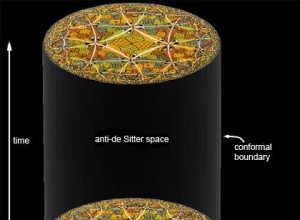
In my last post, I used the GKP-Witten relation ${Z_{CFT}} = {e^{ - {S_{GRAVITY}}}}({\phi _i})$ to solve to ‘Ricci/dilaton‘ problem for the action of supergravity, since the holographic formula derived

${S_A} = \frac{{\left| {{\gamma _A}} \right|}}{{4G_N^3}} = \frac{{\frac{{3R}}{{2G_N^{(3)}}}}}{3}{\rm{log}}\left( {\frac{{{l_s}}}{g}} \right)$

with ${l_s}$ being the string length, allowed us to compute the Matsubara frequencies for the gravitonic wave under the Seiberg quantum fluctuation of the string world-sheet:

${S_\eta } = \frac{1}{\beta }\,{\sum\limits_{\frac{{i2\pi }}{\beta }} {\left( {i\frac{{2n + 1}}{\beta }} \right)} ^\pi }$

$\beta$ being the bosonic frequency. The philosophical problem now is that by the Heisenberg’s Uncertainty Principle for time and energy: ${H_{E,t}}$ , the string time parameter on the world sheet $R_{{S_{({\sigma _s},{\sigma _t})}}}^{2d}$ , ${\sigma _t}$ , goes into quantum superpositionality, and thus ${S_\eta }(n)$ as a function of $n$ runs into the Riemann-Lebesgue Lemma ‘problem’, since the Fourier transform of ${S_\eta }(n)$ , $\mathop {{S_\eta }}\limits^ \sim (n)$ , is such that

$\mathop {{S_\eta }}\limits^ \sim (n) = \int_{ - \infty }^\infty {{e^{i\varphi t}}} {S_\eta }(n)\,dt$

with $\varphi$ real, is NOT convergent since the quantization of spacetime is an anti-smoothing dynamical breaking of the Ricci scalar ${R_{\mu \nu }}$ : hence,

$\int_{ - \infty }^\infty {\left| {{S_\eta }(n)} \right|} \,dt > \infty$

which is incoherent: to see this, note that the anti-smoothing of spacetime implies that ${S_\eta }(n)$ cannot be recovered from $\mathop {{S_\eta }}\limits^ \sim (n)$ via

${S_\eta }(n) = \left( {1/2\pi } \right)\int_{ - \infty }^\infty {{e^{i\varphi t}}} \mathop {{S_\eta }(n)\,d\varphi }\limits^ \sim$

and that implies that the gravitonic wave-propagation travels in spacetime at infinite speed, given

$\int_{ - \infty }^\infty {\left| {{S_\eta }(n)} \right|} \,dt > \infty$

and by quantum wave-particle duality, and the violation of Special Relativity, the graviton provably cannot exist: or, by quantum tunnelling and the fact that gravitons SELF-gravitate, we have the instantaneous collapse of the universe to a zero-dimensional singularity – pick your poison!

A solution I found works is to integrate over orbibolds and derive the supergravity (SuGra) by orbifoidal D-11 and D-10 SuGra actions. So let us see how this works and solves the Riemann-Lebesgue catastrophe via Fourier non-transformation. One must begin by giving a description of the field contents and the degrees of freedom, which will turn out to be a crucial number. At first, one realizes how, in D=11, SuGra theory has a ‘simple’ action: using exterior algebraic notation for the anti-symmetric tensor fields: ${A_3} \equiv 1/3!{A_{3\mu \nu }}\,d{x^\mu }d{x^\nu }d{x^\rho }$ , with the field strength ${F_4} \equiv d{A_3}$ , it is surprisingly

$1.\quad {S_{11}} = \frac{1}{{2\kappa _{11}^2}}\int {\left[ {\sqrt G \left( {{R_G} - \frac{1}{2}{{\left| {{F_4}} \right|}^2}} \right) - \frac{1}{6}{A_3} \wedge {F_4} \wedge {F_4}} \right] + {\rm{fermions}}}$

with $\kappa$ being the Newtonian constant in 11 dimensions. By dimensional reduction, the Type IIA can be derived from $1.$ , but I will not go into that here. Note that there are D=10 supergravity theories with only $N = 11$ SuSy which couple to D=10 super–Yang-Mills theory. We still do not have a workable Type IIB theory since it involves an antisymmetric field $A_4^ +$ with a self-dual field strength. Nonetheless, one may still derive an action that involves both dualities of ${A_4}$ : then, by imposing the self-duality really as a supplementary equation in second-quantization form, thus getting

$\begin{array}{l}2.\quad {S_{IIB}} = + \frac{1}{{4\kappa _B^2}}\int {\sqrt G } {e^{ - 2\Phi }}\left( {2{R_G} + 8{\partial _\mu }\Phi - {{\left| {{H_3}} \right|}^2}} \right)\\ - \frac{1}{{4\kappa _B^2}}\int {\left[ {\sqrt G \left( {{{\left| {{F_1}} \right|}^2} + {{\left| {\mathop {{F_3}}\limits^ \sim } \right|}^2} + A_4^ + \wedge {H_3} \wedge {F_3}} \right)} \right]} + {\rm{ fermions}}\end{array}$

with field strengths: ${F_1} = dC$ , ${H_3} = dB$ , ${F_3} = d{A_2}$ , ${F_5} = dA_4^ +$ , $\mathop {{F_3}}\limits^ \sim = {F_3} - C{H_3}$ , $\mathop {{F_5}}\limits^ \sim = {F_5} - \frac{1}{2}{A_2} \wedge {H_3} + \frac{1}{2}B \wedge {F_3}$ with the self-duality condition $* \mathop {{F_5}}\limits^ \sim = \mathop {{F_5}}\limits^ \sim$ .

Note that the above action arises from the string low energy limit.

${S_{IIB}} = + \frac{1}{{4\kappa _B^2}}\int {\sqrt G } {e^{ - 2\Phi }}\left( {2{R_G} + 8{\partial _\mu }\Phi {\partial ^\mu }\Phi - {{\left| {{H_3}} \right|}^2}} \right)$

naturally deriving the NS-NS sector of the theory, while

$- \frac{1}{{4\pi _B^2}}\int {\left[ {\sqrt G \left( {{{\left| {{F_1}} \right|}^2} + {{\left| {\mathop {{F_3}}\limits^ \sim } \right|}^2}} \right) + A_4^ + \wedge {H_3} \wedge {F_3}} \right]} + {\rm{ fermions}}$

is derivable from the RR sector of the theory. Now, Type IIB supergravity theory is invariant under the NON-compact symmetry group $SU(1,1) \sim SL(2,\mathbb{R})$ and the key is that this symmetry is NOT manifest in

To make it so, one must redefine fields, from the STRING metric ${G_{\mu \nu }}$ in $2$ ., to the Einstein metric ${G_{E\mu \nu }}$ , along with a complexification of the tensor fields

$3.\quad {G_{E\mu \nu }} \equiv {e^{ - \Phi /2}}{G_{\mu \nu }},{\rm{ }}\tau \equiv C + i{e^{ - \Phi }}{\rm{, }}G \equiv \left( {{F_3} - \tau {H_3}} \right)/\sqrt {{\mathop{\rm Im}\nolimits} \tau }$

Now, the action is easily seen to be:

$\begin{array}{c}4.\quad {S_{IIB}} = \frac{1}{{4\kappa _B^2}}\int {\sqrt {{G_E}} } \left( {2{R_{{G_E}}} - \frac{{{\partial _\mu }\mathop \tau \limits^ \sim {\partial ^\mu }\tau }}{{{{\left( {{\rm{Im}}\tau } \right)}^2}}} - \frac{1}{2}{{\left| {{F_1}} \right|}^2} - {{\left| {{G_3}} \right|}^2} - \frac{1}{2}{{\left| {\mathop {{F_5}}\limits^ \sim } \right|}^2}} \right)\\ - \frac{1}{{4i\kappa _B^2}}\int {{A_4}} \wedge \mathop {{G_3}}\limits^ \sim \wedge {G_3}\end{array}$

the metric and $A_4^ +$ fields are invariants under the $SU(1,1) \sim SL(2,\mathbb{R})$ symmetry of Type IIB supergravity. The axionic dilaton field $\tau$ varies with a Möbius super-transformation

$5.\quad \tau \to \tau ' = \frac{{a\tau + b}}{{c\tau + d}}{\rm{ }}\quad ad - bc = 1\,{\rm{, }}\,a,\,b,\,c,\,d \in \mathbb{R}$

and ${A_{2\mu \nu }}$ , ${B_{\mu \nu }}$ self-rotate under the Möbius super-transformation, and can most clearly be visualized as a complex 3-form field ${G_3}$

$6.\quad {G_3} \to G_3^\dagger = \frac{{c{\tau ^\dagger } + d}}{{\left| {c\tau + d} \right|}}{G_3}$

The SuSy transformation for Type IIB supergravity on the fermion fields are of the following form, via Seiberg–Witten analysis, without a need for bosonic transformation laws, with the dilaton $\lambda$ and the gravitino ${\psi _M}$

$\begin{array}{c}7.\quad \delta \lambda = \frac{i}{{{\kappa _B}}}{\Gamma ^\mu }{\eta ^ * }\frac{{{\partial _\mu }\tau }}{{{\rm{Im}}\tau }} - \frac{i}{{24}}{\Gamma ^{\mu \nu \rho }}\eta {G_{3\mu \nu \rho }} + {\left( {{\rm{fermi}}} \right)^2}\\\delta {\psi _\mu } = \frac{1}{{{\kappa _B}}}{D_\mu }\eta + \frac{1}{{480}}{\Gamma ^{\mu 1...\mu 5}}{\Gamma _\mu }\eta {F_{5\mu 1...\mu 5}} + \frac{1}{{96}}\left( {\Gamma _\mu ^{\rho \sigma \tau }{G_{3\rho \sigma \tau }} - 9{\Gamma ^{\nu \rho }}} \right){\eta ^ * }\\ + \,{{\rm{(Fermi)}}^2}\end{array}$

It is crucial to realize that in the $SU(1,1)$ context, the supersymmetry transformation parameter $\eta$ essentially has $1/2{\rm{ }}\;U(1)$ charge, implying that $\lambda$ has necessarily, given unitarity, $3/2$ and ${\psi _\mu }$ has $1/2$ .

The geometry of superstring theory in the Ramond-Neveu-Schwarz (RNS) setting are the bosonic world sheet fields $x_{WS}^\mu$ and the fermionic world sheet fields $\psi _ \pm ^\mu$ , with $\pm$ expressing chirality, and $x_{WS}^\mu$ , $\psi _ \pm ^\mu$ must be viewed as functions of local worldsheet coordinates ${\xi ^1}\,,{\rm{ }}\,{\xi ^2}$ in order for quantum fluctuation of both world sheets of the open and closed strings to give rise to the graviton via axionic current creation/annihilation Hilbert operators acting on string vacua. Both $x_{WS}^\mu$ and $\psi _ \pm ^\mu$ vectorially transform under the irreducible representation of the spacetime Lorentz group. By using ‘Gliozzi-Scherk-Olive‘ holographic projections, the spacetime supersymmetric derivative can ‘act‘ on the $1.$ and $2.$ actions above! It is more philosophically informative to work with orientable strings: now, the Type II and heterotic string theories are perfectly suited in this context. Field interactions in second quantization arise from the orbifoidal splitting and joining of the worldsheets, and causality is maintained: moreover, the genus for orientable worldsheets equals the number of Witten-handles. The world sheet bosonic field $x_{WS}^\mu$ naturally gives rise to a non-linear sigma model

$8.\quad {S_{x_{WS}^\mu }} = \frac{1}{{4\pi {\alpha ^ * }}}\int_\Sigma {\sqrt \gamma } \left[ {\left\{ {{\gamma ^{mn}}{G_{\mu \nu }}(x_{WS}^\mu ) + {\varepsilon ^{mn}}{B_{\mu \nu }}(x_{WS}^\mu )} \right\}{\partial _m}{x^{\mu \dagger }}{\partial _n}{x^{\nu \dagger }} + {\alpha ^\dagger }R_\gamma ^{(2)}\Phi (x_{WS}^\mu )} \right]$

with ${\alpha ^\dagger }$ being the square root of the Planck length, ${\gamma ^{mn}}$ being the worldsheet metric, and $R_\gamma ^{(2)}$ being Gaussian curvature. The worldsheet fermionic field $\psi _ \pm ^\mu$ axially gives rise to a worldsheet supersymmetric completion of the sigma model. It suffices to give its form on a flat worldsheet metric with a vanishing worldsheet gravitino field:

$9.\quad {S_\psi } = \frac{1}{{4\pi {\alpha ^\dagger }}}\int_\Sigma {{d^2}} \xi \left( {{G_{\mu \nu }}(x)\left( {\psi _ + ^\mu {D_{{\gamma _A}}}\psi _ + ^\nu + \psi _ - ^\mu {D_{{\gamma _A}}}\psi _ - ^\nu } \right) + \frac{1}{2}{R_{\mu \nu \rho \sigma }}\psi _ + ^\mu \psi _ + ^\nu \psi _ - ^\rho \psi _ - ^\sigma } \right)$

and ${R_{\mu \nu \rho \sigma }}$ being the Riemann tensor for the metric ${G_{\mu \nu }}$ . Now the all too important SuSy-covariant derivatives can be derived:

$10.1\quad {}^s{D_{{\gamma _A}}}\psi _ + ^\mu = {\partial _{{\gamma _A}}}\psi _ + ^\mu + \left( {\Gamma _{\rho \sigma }^\mu (x) + \frac{1}{2}H{{_3^\mu }_{\rho \sigma }}(x)} \right){\partial _{{\gamma _A}}}{x^\rho }\psi _ + ^\sigma$

$10.2\quad {D_{{\gamma _A}}}\psi _ - ^\mu = {\partial _{{\gamma _A}}}\psi _ - ^\mu + \left( {\Gamma _{\rho \sigma }^\mu (x) - \frac{1}{2}H{{_3^\mu }_{\rho \sigma }}(x)} \right){\partial _{{\gamma _A}}}{x^\rho }\psi _ - ^\sigma$

with $\Gamma _{\rho \sigma }^\mu$ being the Levi-Civita connections for $G$ . Now one is in a position to solve the Riemann-Lebesgue/Fourier anomaly via the functional integral over all $x_{W{S_i}}^\mu$ and ${\psi _ \pm }$ by integrating over all worldsheet metrics ${\gamma ^{mn}}$ and worldsheet gravitini fields ${\chi _m}$ via the amplitude

$\begin{array}{c}{\rm{11}}.\quad {\rm{amplititude}}{\mkern 1mu} = \\\sum\limits_{{\rm{topologies/orbifolds}}} {\int {D{\gamma ^{mn}}} } D{\chi _m}\int D x_{WS}^\mu D\psi {e^{ - {S_x} + {S_\psi }}}\end{array}$

This clearly solves the Feynman propagation problem. And the upshot is that the vacuum expectation value of the dilaton field is $\phi = \left\langle \Phi \right\rangle$ , and the string vacuum expectation value to the string amplitude is, magically, given by the Euler number ${\chi ^{(\Sigma )}}$ of the world sheet $R_{{S_{({\sigma _s},{\sigma _t})}}}^{2d}$

$12.\quad \frac{1}{{2\pi }}\int_{R_{{S_{({\sigma _s},{\sigma _t})}}}^{2d}} {\sqrt \gamma } {R^{(2)}}_{{\gamma _A}} = {\chi ^{(\Sigma )}} = 2 - 2h - b$

with $h$ is the genus, $b$ is a number that counts the orbifoidal puntures in spacetime as the string world sheet propagates under quantum fluctuations. Thus, a genus $h$ world sheet with no boundary gets a multiplicative contribution: ${e^{ - (2 - 2h)\phi }} = g_s^{2h - 2}$ , thus deriving another magical identity, ${g_s} = {e^\phi }$ , representing the closed string coupling constant which lives on a D-brane (for another post), and hence via the SuSy action and the creation/annihilation Hilbert operator, one has a finite, causal quantum SuGra actions in D=11/ D=10.

Next, I should convince you that Conformal Invariance is satisfied in the AdS/CFT setting and that Supergravity Field Equations have solutions, but at a high ontological price!