A natural and intuitive way of deriving the standard inflationary ΛCDM cosmological model is by identifying the Type-IIB Kähler modulus with the ΛCDM-inflaton. The ![]() -brane interaction is of particular importance because the worldvolume theory on a stack of
-brane interaction is of particular importance because the worldvolume theory on a stack of ![]() -branes probing a Calabi-Yau 3-fold is a 4-D
-branes probing a Calabi-Yau 3-fold is a 4-D ![]() supersymmetric gauge theory and the importance of a
supersymmetric gauge theory and the importance of a ![]() worldvolume theory derives, via duality-relations, from F-theory compactification by availing ourselves to the heterotic/F-theory duality in eight dimensions. Generally, for a
worldvolume theory derives, via duality-relations, from F-theory compactification by availing ourselves to the heterotic/F-theory duality in eight dimensions. Generally, for a ![]() -brane,
-brane, ![]() , there naturally is a
, there naturally is a ![]() -D
-D ![]() SYM theory associated with its
SYM theory associated with its ![]() worldvolume
worldvolume ![]() , where the Dirac-Born-Infeld action is given by:
, where the Dirac-Born-Infeld action is given by:
![]()
coupled to a Chern-Simons Wess-Zumino term:
![]()
![]() the worldvolume
the worldvolume ![]() pullback, and the corresponding p-orientifold action is:
pullback, and the corresponding p-orientifold action is:
![]()
with the string-coupling given by:
![]()
![]() and
and ![]() the pullbacks SUGRA fields to the
the pullbacks SUGRA fields to the ![]() -brane worldvolume. Thus, we can derive the action:
-brane worldvolume. Thus, we can derive the action:
![]()
with:
![]()
![]()
![]()
which yields a 10-D SYM action:
![]()
with:
![]()
and ![]() the non-abelian field strength of the
the non-abelian field strength of the ![]() gauge field
gauge field ![]() :
:
![]()
where the gauge covariant derivative is defined by:
![]()
giving us the ![]() -worldvolume SYM action:
-worldvolume SYM action:
![]()
with:
![]()
![]()
![]()
![]()
with the potential:
![]()
that will figure in the Kähler form that will characterize ![]() -brane cosmology.
-brane cosmology. ![]() -branes are central not simply because of F-theory compactification due to
-branes are central not simply because of F-theory compactification due to ![]() backreaction and Type-IIB axio-dilaton, but also because the Kähler moduli space induced by the
backreaction and Type-IIB axio-dilaton, but also because the Kähler moduli space induced by the ![]() -brane F-theoretic backreaction has a modulus that can naturally be identified with the ΛCDM-inflaton. Thus, inflationary cosmology can be derived, up to isomorphism, from 6D F-theory compactification using the Type-IIB string-theory/11D SUGRA duality upon dimensional reduction to 4D, where the Type-IIB SUGRA action in the string frame is given by:
-brane F-theoretic backreaction has a modulus that can naturally be identified with the ΛCDM-inflaton. Thus, inflationary cosmology can be derived, up to isomorphism, from 6D F-theory compactification using the Type-IIB string-theory/11D SUGRA duality upon dimensional reduction to 4D, where the Type-IIB SUGRA action in the string frame is given by:
![]()
with:
![]()
![]()
![]()
In light of flux moduli stabilization, this is a natural framework since the Kähler moduli potential apriori allows a Type-IIB-modulus/ΛCDM-inflaton identification. In such a SYM ![]() -brane scenario, we have an
-brane scenario, we have an ![]() -flaton model in the Large Volume Scenario that evades the
-flaton model in the Large Volume Scenario that evades the ![]() -problem, and periodicity of the modulus is achieved by defluxing the pullback of the
-problem, and periodicity of the modulus is achieved by defluxing the pullback of the ![]() -term on the superstring worldsheet. This can be readily seen since the total supersymmetric worldsheet action in conformal gauge:
-term on the superstring worldsheet. This can be readily seen since the total supersymmetric worldsheet action in conformal gauge:
![]()
with:
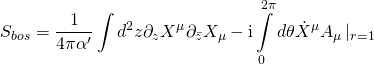
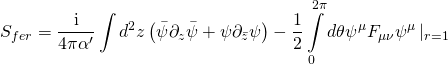
has modular-invariance. The skeleton of ![]() Type-IIB flux compactification on a Calabi-Yau threefold
Type-IIB flux compactification on a Calabi-Yau threefold ![]() is constructed from a superpotential of the form:
is constructed from a superpotential of the form:
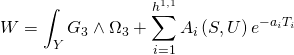
where:
![]()
is the Gukov-Vafa-Witten superpotential stabilization complex term, as well as the axio-dilaton field:
![]()
Given the presence of ![]() -brane instantons,
-brane instantons, ![]() are of Kähler moduli Type-IIB-orbifold class:
are of Kähler moduli Type-IIB-orbifold class:
![]()
with ![]() being the volume of the divisor
being the volume of the divisor ![]() and
and ![]() the 4-form Ramond-Ramond axion field corresponding to:
the 4-form Ramond-Ramond axion field corresponding to:
![]()
and:
![]()
where ![]() is the Kähler form:
is the Kähler form:
![]()
and:
![]()
an integral-form basis and ![]() the associated intersection coefficients. Hence, the Kähler potential is given by:
the associated intersection coefficients. Hence, the Kähler potential is given by:
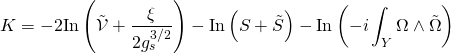
with ![]() the Calabi-Yau volume, and in the Einstein frame, is given by:
the Calabi-Yau volume, and in the Einstein frame, is given by:
![]()
The ![]() -term is given by:
-term is given by:
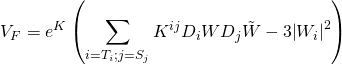
and in the large volume scenario (LVS) is:
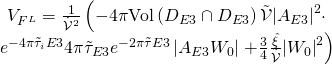
Thus, the LVS ![]() -term is given by:
-term is given by:
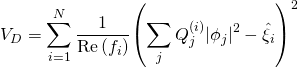
with:
![]()
and the Fayet-Illopoulos terms being:
![]()
where ![]() are the
are the ![]() -brane charge-vectors. The Kähler LVS potential is now derivable, and takes the form:
-brane charge-vectors. The Kähler LVS potential is now derivable, and takes the form:
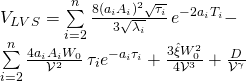
One can now choose any ![]() as the Kähler-modulus-inflaton, and inflation takes place in:
as the Kähler-modulus-inflaton, and inflation takes place in:
![]()
We can build our model now from the Kähler form and the superpotential. For a Witten-deformed ![]() -brane, the Kähler potential is thus derivable in the weak string-coupling limit of the F-theory Kähler potential arising from the elliptic fibration base Calabi-Yau four-fold:
-brane, the Kähler potential is thus derivable in the weak string-coupling limit of the F-theory Kähler potential arising from the elliptic fibration base Calabi-Yau four-fold:
![]()
Expanded in the weak string coupling limit gives us:
![]()
with ![]() the periods of integrals of the holomorphic (3,0)-form over the symplectic basis of 3-cycles with intersection matrix
the periods of integrals of the holomorphic (3,0)-form over the symplectic basis of 3-cycles with intersection matrix ![]() and
and ![]() is a function of symplectic and brane-moduli that figures in the flux-compactification moduli-stabilization but is independent of the axio-dilaton. Using mirror symmetry, the Kähler potential:
is a function of symplectic and brane-moduli that figures in the flux-compactification moduli-stabilization but is independent of the axio-dilaton. Using mirror symmetry, the Kähler potential:
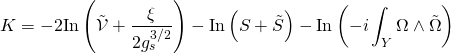
can be identified with the Kähler-moduli-potential of the mirror fourfold, which in the LVS-limit, involves the volume moduli of the elliptic fourfold, but not the corresponding axions due to shift-symmetry. Hence, the shift-invariant potential takes the form:
![]()
![]() the self-intersecting matrix of the mirror four-fold divisors and
the self-intersecting matrix of the mirror four-fold divisors and ![]() the complex structure of the moduli of the three-form. We can now identify any
the complex structure of the moduli of the three-form. We can now identify any ![]() with the axio-dilaton and the remaining identified with the
with the axio-dilaton and the remaining identified with the ![]() -brane position-moduli
-brane position-moduli ![]() and the three-fold complex moduli
and the three-fold complex moduli ![]() . Their interdependence can be expressed by the relation:
. Their interdependence can be expressed by the relation:
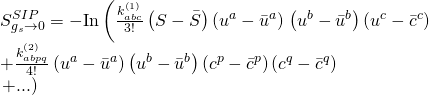
Hence, any ![]() can be identified with the deformation complex moduli term
can be identified with the deformation complex moduli term ![]() of a
of a ![]() -brane, and Type-IIB N-flaton cosmology can reproduce ΛCDM by integrating out all the other moduli terms, and by substitution, the Kähler potential:
-brane, and Type-IIB N-flaton cosmology can reproduce ΛCDM by integrating out all the other moduli terms, and by substitution, the Kähler potential:
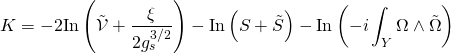
takes the following form:
![]()
The F-theory backreacted counterpart Kähler potential hence takes the form:
![]()
where ![]() are the flux compactification quantum numbers and
are the flux compactification quantum numbers and ![]() is the period four-fold Calabi-Yau vector. In terms of the brane modulus
is the period four-fold Calabi-Yau vector. In terms of the brane modulus ![]() , we can write the potential as:
, we can write the potential as:
![]()
We now include the Kähler moduli term to the potential:
![]()
and the superpotential:
![]()
Then, instanton correction terms from the four-fold blow-up cycles yield:
![]()
from which the F-term potential:
![]()
can be derived. ![]() the complexified Kähler moduli that measure the 3-fold four-cycles when restricted to the reals, in string-length unit measure and as standard,
the complexified Kähler moduli that measure the 3-fold four-cycles when restricted to the reals, in string-length unit measure and as standard, ![]() the Calabi-Yau 3-fold volume. Now since the Kähler metric is block-diagonal in the total space, no mixed derivatives in
the Calabi-Yau 3-fold volume. Now since the Kähler metric is block-diagonal in the total space, no mixed derivatives in ![]() and
and ![]() occur in:
occur in:
![]()
hence the term ![]() in the F-term potential dominates and stabilizes
in the F-term potential dominates and stabilizes ![]() in a supersymmetric minimum:
in a supersymmetric minimum:
![]()
Thus, we have a classic moduli stabilization and applies to our Large Volume Scenario straightforwardly and yields the ![]() minimum:
minimum:
![]()
that can be uplifted to a Minkowski minimum. Since inflation occurs in ![]() and the terms:
and the terms:
![]()
are subleading in the inverse of ![]() with respect to
with respect to ![]() , it follows that the leading inflaton mass term is part of:
, it follows that the leading inflaton mass term is part of:
![]()
Since the LVS large-scale structure of the Kähler moduli space guarantees that loop-corrections are stably subleading with respect to ![]() moduli-stabilization
moduli-stabilization ![]() -corrections, the Type-IIB axio-dilaton and brane moduli are integrated out at higher scales. Central is the
-corrections, the Type-IIB axio-dilaton and brane moduli are integrated out at higher scales. Central is the ![]() -stabilization, since from:
-stabilization, since from:
![]()
we can derive:
![]()
with ![]() . At the ground level,
. At the ground level,
![]()
vanishes and we have:
![]()
and imposing the condition that the real part of:
![]()
at first-order in the ![]() and
and ![]() terms vanishes gives us:
terms vanishes gives us:
![]()
We are now in position to derive the inflaton mass which arises from:
![]()
Moreover, in the minimum, we have:
![]()
and given that the Chern-Simons orientifold action gets the following Calabi-Yau curvature-correction:
![Rendered by QuickLaTeX.com \displaystyle {{S}_{{{{O}_{p}},CS}}}=-{{2}^{{p-4}}}-{{T}_{p}}\int_{{{\mathcal{W}}'}}{{P\left[ C \right]}}\wedge \sqrt{{\frac{{L\left( {\frac{1}{4}{{{\left( {2\pi } \right)}}^{2}}{\alpha }'T{\mathcal{W}}'} \right)}}{{L\left( {\frac{1}{4}{{{\left( {2\pi } \right)}}^{2}}{\alpha }'N{\mathcal{W}}'} \right)}}}}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-66b2c5ec103f848b0b3b14b367eed67b_l3.png)
we hence only need to expand it in the leading order with respect to the real part ![]() and moduli stabilization enforces
and moduli stabilization enforces ![]() which scales linearly. Hence we have:
which scales linearly. Hence we have:
![]()
and:
![]()
Thus, the SM renormalization parameter connects the inflaton to ![]() . Since the kinetic term for
. Since the kinetic term for ![]() is contained in:
is contained in:
![]()
then from:
![]()
and:
![]()
we can deduce:
![]()
In the ΛCDM Standard Model, quadratic inflation has a potential ![]() with slow-roll parameters obeying the following relations:
with slow-roll parameters obeying the following relations:
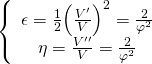
with spectral index:
![]()
Phenomenologically, the ΛCDM Standard Model sets this term at ![]() with e-fold field displacement
with e-fold field displacement ![]() and
and ![]() . Moreover, the amplitude of the curvature perturbations (chapter 2/2.11) yields
. Moreover, the amplitude of the curvature perturbations (chapter 2/2.11) yields ![]() and hence we have
and hence we have ![]() .
.
In Type-IIA/B string theories in the LVS, this remarkably yields:
![]()
In order not to destroy the moduli stabilization, we impose the harmless condition:
![]()
along the inflaton field flow. Now during the inflationary phase, we have:
![]()
and the imaginary part does not destroy moduli stability since:
![]()
holds, giving:
![]()
and since the LVS F-term is given by:
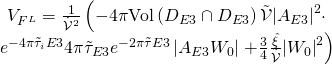
we have:
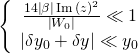
To handle the cubic and quartic terms in ![]() , we expand:
, we expand:
![]()
in ![]() where at the minimum we have:
where at the minimum we have:
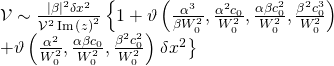
Solving:
![]()
with respect to ![]() gives us:
gives us:
![]()
and:
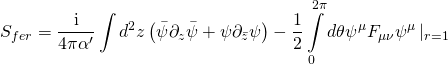
with respect to the kappa symmetric shift Type-IIB parameter, we get the Type-IIA dual instanton alpha-corrections to the Kähler potential thus yielding the correct Hilbert inflaton spectrum correction to the F-term:
![]()
Now, given:
![]()
the Kaluza-Klein inter-brane mode loop corrections give us the correct periodicity condition:
![]()
due to the Gauss–Codazzi equations for:
![]()
and are parametrized as:
![]()
at leading order. Since axion decay always takes place in a small region in e-fold inflation and is bounded by ![]() , then during the initial e-folding stage, under the Kähler-modulus/inflaton identification, the inflaton crosses at least once the period of the oscillatory term of:
, then during the initial e-folding stage, under the Kähler-modulus/inflaton identification, the inflaton crosses at least once the period of the oscillatory term of:
![]()
and hence for large ![]() and small
and small ![]() and
and ![]() , the Type-IIB 4-D SUGRA Kähler modulus under such inflaton-identification reproduces the ΛCDM Standard Model mainly because, as a Dirac variety, a D7-brane encircles a closed trajectory in Kähler moduli space enough times in the slow-roll scape to grow a contribution to the F-term potential that appears in the action of Type-IIB 4-D SUGRA. The phenomenological aspects of such claims can be computed from this source.
, the Type-IIB 4-D SUGRA Kähler modulus under such inflaton-identification reproduces the ΛCDM Standard Model mainly because, as a Dirac variety, a D7-brane encircles a closed trajectory in Kähler moduli space enough times in the slow-roll scape to grow a contribution to the F-term potential that appears in the action of Type-IIB 4-D SUGRA. The phenomenological aspects of such claims can be computed from this source.
