No non-poetic account of reality can be complete. ~ John Myhill! Indeed, for mathematical physics has become a form of abstract poetry!
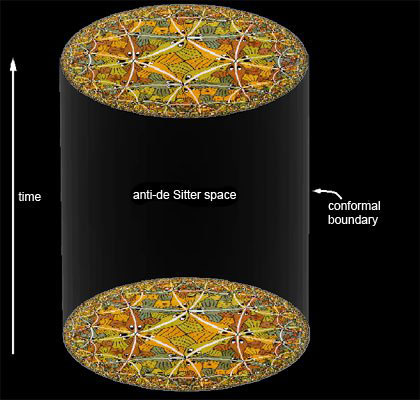
In this post, I should convince you, as I said in my last post, that Conformal Invariance is satisfied in the AdS/CFT setting and that Supergravity Field Equations have solutions, but at a high ontological price, and that price involves p and D Branes. More on those exotic entities in a bit. We also saw that the non-linear sigma model, as a 2-Dimensional quantum field theory, can be interpreted for any background field content and strength. However, when the non-linear sigma model is to give rise to a consistent string theory where the Feynman path summation
![]()
can be ‘summed’ over degenerate topologies and in order for the Polyakov string worldsheet action
![Rendered by QuickLaTeX.com \[2.\quad \frac{1}{{2\pi }}\int_{R_{{S_{({\sigma _s},{\sigma _t})}}}^{2d}} {\sqrt {{\gamma _A}} } {R^{(2)}}_{{\gamma _A}} = {\chi ^{(\sum )}} = 2 - 2h - b\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-8fccf5e1d206f0d44e36d729b7d8bc1f_l3.png)
to have solution(s), where ![]() is the Euler number of
is the Euler number of ![]() ,
, ![]() the genus, and
the genus, and ![]() counts the quantum spacetime punctures corresponding to the topological entropic fluctuations of the holes of the propagation current of closed strings, one must satisfy additional physical conditions: most essential being that the string spectrum be free of negative norm states. Those states always occur because the Poincaré invariance of the theory forces the string map
counts the quantum spacetime punctures corresponding to the topological entropic fluctuations of the holes of the propagation current of closed strings, one must satisfy additional physical conditions: most essential being that the string spectrum be free of negative norm states. Those states always occur because the Poincaré invariance of the theory forces the string map ![]() to satisfy the canonical relation
to satisfy the canonical relation
![]()
and hence ![]() creates a negative norm. I will get back to this point, but at this juncture, I need to introduce the notion of p and D Branes and state the essential facts about them, since they will provide the ultimate ontology of any consistent quantum field theory of gravity. A brane is a topological generalization of point-particles to higher dimensions. A point particle is thus a brane with zero dimension, a string is a brane with one dimension and so on…, but for D = 10/D = 11 supergravity, one needs higher dimensional Branes. So: a
creates a negative norm. I will get back to this point, but at this juncture, I need to introduce the notion of p and D Branes and state the essential facts about them, since they will provide the ultimate ontology of any consistent quantum field theory of gravity. A brane is a topological generalization of point-particles to higher dimensions. A point particle is thus a brane with zero dimension, a string is a brane with one dimension and so on…, but for D = 10/D = 11 supergravity, one needs higher dimensional Branes. So: a ![]() is a
is a ![]() in
in ![]() . Dynamically, a
. Dynamically, a ![]() propagates through spacetime and sweeps a
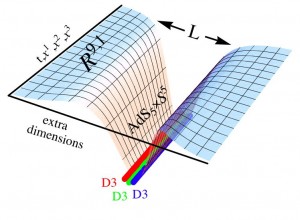
propagates through spacetime and sweeps a ![]() worldvolume. In the AdS/CFT correspondence context, since in the left hand side of the duality
worldvolume. In the AdS/CFT correspondence context, since in the left hand side of the duality
![Rendered by QuickLaTeX.com \[\begin{array}{c}{\left\langle {\Im \left\{ {\exp \left( {\int {{d^4}{J_{4D}}(X)\vartheta (x)} } \right)} \right\}} \right\rangle _{CFT}} = \\{Z_{AdS}}\left[ {\frac{{{\rm{lim}}}}{{{\rm{boundary}}}}J{\omega ^{\Delta - d + k}} = {J_{4D}}} \right]\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-75ec75ab97ee8b1881dbe9e462297cf5_l3.png)
the open strings represents the gauge theory, they are bounded by ![]() (for Dirichlet), which are topological ‘parametric’ boundary condition for their endpoints. Here are the main and essential facts about Branes: consider a
(for Dirichlet), which are topological ‘parametric’ boundary condition for their endpoints. Here are the main and essential facts about Branes: consider a ![]() in Euclidean space with corresponding topological distance
in Euclidean space with corresponding topological distance ![]() . The trace over states in the
. The trace over states in the ![]() amplitudes for open strings is
amplitudes for open strings is
![]()
![]() being the supercharge, and the power of
being the supercharge, and the power of ![]() arises from the momentum integral
arises from the momentum integral
![]()
so we get
![Rendered by QuickLaTeX.com \[\begin{array}{c}5.\quad {A_{p - L}} = C\,\int_0^\infty {\frac{{dt}}{{{t^p}}}} {(8{\pi ^p}{\alpha ^\dagger }t)^{(q - p)}}\exp \left( { - \frac{{t{y^p}}}{{2\pi {\alpha ^\dagger }}}} \right)\\ \sim {y^{ - (7 - p)}} \sim G_{9 - p}^{(y)}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d9442a5030f17960f14aca1e3e458505_l3.png)
with ![]() being the scalar Green’s functions in
being the scalar Green’s functions in ![]() . Now one is in a position to derive the action for
. Now one is in a position to derive the action for ![]()
![]()
which generalizes, in the AdS/CFT bulk theory to
![]()
where ![]() reflects the fact that in the open string sector, the coupling constant is the square root of the closed string: since the open string represents the gauge theory, and the closed string the gravity part on the AdS boundary, we have a quantum field theoretic gauge invariant description of quantized gravity and thus spacetime. Now back to the ‘negative norm’ problem mentioned on top.
reflects the fact that in the open string sector, the coupling constant is the square root of the closed string: since the open string represents the gauge theory, and the closed string the gravity part on the AdS boundary, we have a quantum field theoretic gauge invariant description of quantized gravity and thus spacetime. Now back to the ‘negative norm’ problem mentioned on top.
One can decouple such a negative norm via conformal invariance, out of the Fock space, of the non-linear sigma model. So, conformal invariance necessitates worldsheet invariance of the full quantum field theoretic non-linear sigma model. Such transformations of the worldsheet scale ![]() are spontaneously broken by quantum anomalies of the super-axion current, and whose content is entropically encoded by the
are spontaneously broken by quantum anomalies of the super-axion current, and whose content is entropically encoded by the ![]() function of the renormalization group. Each background field must have a
function of the renormalization group. Each background field must have a ![]() function and worldsheet scale
function and worldsheet scale ![]() with conformal invariance – thus implying the vanishing of the
with conformal invariance – thus implying the vanishing of the ![]() function. The background fields
function. The background fields ![]() ,
, ![]() , and
, and ![]() are generating functions for an infinite series of coupling constants for the metric, and hence one can derive
are generating functions for an infinite series of coupling constants for the metric, and hence one can derive
![Rendered by QuickLaTeX.com \[7.\quad {G_{\mu \nu }}(x) = \sum\limits_{n = 0}^\infty {\frac{1}{{n!}}} {(x - {x_0})^{{\mu _1}}}...{(x - {x_0})^{{\mu _n}}}{\partial _{{\mu _1}}}...{\partial _{{\mu _n}}}{G_{\mu \nu }}({x_0})\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c8333228e8f011ec7c4a9fa1b0366dc2_l3.png)
where ![]() are Taylor expansion coefficients and are an independent set of super-Yukawa couplings, and give rise to the irreducible representation of the renormalization group, and therefore ‘flow’: and this infinite number of coupling-flows surjectively flow into themselves. Thus, they can be redefined by generating functions
are Taylor expansion coefficients and are an independent set of super-Yukawa couplings, and give rise to the irreducible representation of the renormalization group, and therefore ‘flow’: and this infinite number of coupling-flows surjectively flow into themselves. Thus, they can be redefined by generating functions
![]()
definable for the metric via
![Rendered by QuickLaTeX.com \[8.\quad \beta _{\mu \nu }^G(x) = \frac{{\partial {G_{\mu \nu }}}}{{\partial {\rm{In}}\Lambda }} \equiv \sum\limits_{n = 0}^\infty {\frac{1}{{n!}}} {(x - {x_0})^{{\mu _1}}}...\,{(x - {x_0})^{{\mu _n}}}\frac{{{\partial _{{\mu _1}}}{G_{\mu \nu }}(x)...{\partial _{{\mu _n}}}{G_{\mu \nu }}({x_0})}}{{\partial \,{\rm{In}}\,\Lambda }}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e805a89d75b87ba7600684fc70a65afb_l3.png)
Now, when one has an infinite number of coupling constants that occur in a quantum field theory, it is apriori non-renormalizable, since a prediction based on a quantum measurement of a physical ‘observable’ (in the Hilbert space sense) would need an infinite number of data to be localized at a single spacetime point, which is incoherent!
This is again where string theory comes to the rescue. One can assume that the total renormalization process of the non-linear sigma model preserves diffeomorphism invariance of spacetime: then, the number of field strength terms that appear in the renormalization group ‘flow’ is order-by-order finite in the ![]() expansion. Moreover, the presence of an infinite number of Yukawa couplings allows for the possibility of the string propagation (line: # 1. on top) to occur in an infinite family of spacetimes: in this setting, the leading order
expansion. Moreover, the presence of an infinite number of Yukawa couplings allows for the possibility of the string propagation (line: # 1. on top) to occur in an infinite family of spacetimes: in this setting, the leading order ![]() functions are
functions are
![]()
![]()
![]()
Note now that the scale invariance, by dimensional analysis, reduces to supergravity field equations. To go further, we need Brane ontology and the properties of Branes stated in (3.), through (6.1.) above. Here is the nice story:
In supergravity, an anti-symmetric rank p+1 tensor field ![]() can be identified with a (p+1)-form
can be identified with a (p+1)-form
![]()
which couples to topological entities: ![]() of spacetime dimension p+1, given that one can derive the diffeomorphism invariant action
of spacetime dimension p+1, given that one can derive the diffeomorphism invariant action
![Rendered by QuickLaTeX.com \[11.\quad {S_{p + 1}} = {T_{p + 1}}\int_{{\Sigma _{p + 1}}\left( {x_{{\Sigma _{p + 1}}}^{{\mu ^{p + 1}}}} \right)} {{A_{p + 1}}} \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-b9ec8327abf57ebddf15f5813eb1f79e_l3.png)
which is invariant under Abelian gauge transformation ![]() of rank
of rank ![]()
![]()
since by unitarity, ![]() transforms with the supersymmetric covariant derivatives
transforms with the supersymmetric covariant derivatives
![]()
and
![]()
Now the fields ![]() must have a gauge invariant field strength
must have a gauge invariant field strength ![]() , a p+2 form with flux-conservation property. Now, the magic of mathematics strikes again: the ONLY solutions to the D = 10/D = 11 supergravity actions with non-trivial
, a p+2 form with flux-conservation property. Now, the magic of mathematics strikes again: the ONLY solutions to the D = 10/D = 11 supergravity actions with non-trivial ![]() charge are necessarily
charge are necessarily ![]() !
!
Now, every ![]() gauge field has a magnetic dual
gauge field has a magnetic dual ![]() , essentially a differential form field of rank
, essentially a differential form field of rank ![]() with field strength related to
with field strength related to ![]() via Poincaré Duality
via Poincaré Duality
![]()
and by the Seiberg-Witten prepotential via instanton counting ‘number‘, every
![]()
has a magnetic dual ![]() which couples to
which couples to ![]() .
.
However, ![]() in D = 11 Dimension supergravity are highly unique because the only anti-symmetric tensor field in the supergravity theory IS
in D = 11 Dimension supergravity are highly unique because the only anti-symmetric tensor field in the supergravity theory IS ![]() with rank 3, and thus one can have a
with rank 3, and thus one can have a ![]()
![]() with its magnetic dual
with its magnetic dual ![]() . The
. The ![]() in Type II A/B theory are differentiated as follows: when the anti-symmetric fields with charge is in the RR sector, the
in Type II A/B theory are differentiated as follows: when the anti-symmetric fields with charge is in the RR sector, the ![]() becomes a Dirichlet
becomes a Dirichlet ![]() and will play a central role in the AdS/CFT holographic elimination of gravity via entropic quantum fluctuations on the CFT boundary. Note that quantum entanglement of
and will play a central role in the AdS/CFT holographic elimination of gravity via entropic quantum fluctuations on the CFT boundary. Note that quantum entanglement of ![]() with gravitonic wave propagation on the conformal CFT boundary with NO gravity
with gravitonic wave propagation on the conformal CFT boundary with NO gravity
by itself completes the holographic analysis by substituting ![]() for
for ![]() in
in
![]()
which, by the GKP-Witten relation: ![]() , gives us
, gives us
![]()
Hence, by the Dirichlet boundary condition applied to AdS space, ![]() of dimension 4+p or higher are the only ontolological entities that can be construed as ‘real‘: all else is entropic holomorphic ‘illusions’ arising from Matsubara frequencies of
of dimension 4+p or higher are the only ontolological entities that can be construed as ‘real‘: all else is entropic holomorphic ‘illusions’ arising from Matsubara frequencies of ![]() as they propagationally generate ‘worldvolumes‘. Happy ending: that implies, by General Relativity, that ‘space‘ and ‘time‘ are illusions as well – John Locke was right after all. Next, I shall explore how
as they propagationally generate ‘worldvolumes‘. Happy ending: that implies, by General Relativity, that ‘space‘ and ‘time‘ are illusions as well – John Locke was right after all. Next, I shall explore how ![]() solutions figure in supergravity equations.
solutions figure in supergravity equations.