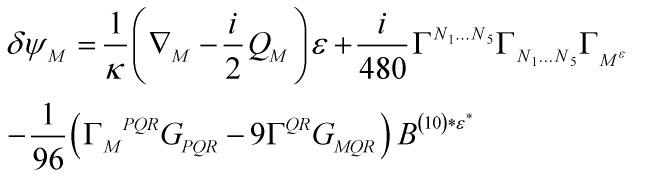In this post, I will analyse several deep issues pertaining to flux compactifications of string theory, and draw foundational conclusions in relation to Kähler and Calabi–Yau manifolds. I already discussed the connection with Hodge theory and Gromov-Witten invariants of Calabi-Yau 3-Folds. The key thing to realize is that fluxes present in 10/11-D string theory naturally stabilize the moduli of a compactification with a downward reduction to 4-dimensional Minkowskian manifolds with broken supersymmetry minimally affecting the quantum vacuum energy as well as a ‘natural’ non-fine-tuned solution to the hierarchy problem: that is their importance for phenomenology, not just theory. Start with the ten-dimensional type IIB supersymmetry transformations:
and:
![]()
with the Gromov-Witten genus-one amplitude given by:
![Rendered by QuickLaTeX.com \[{A^{g = 1}} = {\hat R^4}\int_{{{\hat F}_{\left( 1 \right)}}} {\frac{{{d^2}\tau }}{{\tau _2^2}}} \int_{\hat {\rm T}} {\prod\limits_{i = 1}^3 {\frac{{{d^2}{\nu ^{\left( i \right)}}}}{{{\tau _2}}}} } \,{e^{{D_{\left( 1 \right)}}}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d091fd1cb864904a14c6df6a85d9fa40_l3.png)
with the flux U-duality integral:
![]()
and:
![]()
Fluxes in four-dimensional space–times are clearly central for phenomenological reasons, however, in six dimensions, flux backgrounds are solutions of string theory and induce internal four-dimensional manifolds with flux solutions that are uniquely constrained. Backgrounds with torsion in the connection appear analytically with the torsion being turned on by the three-form tensor field H with property:
![]()
and since the fundamental form of the internal complex n-manifold
![]()
satisfies both:
![]()
and
![]()
we have supersymmetry-preservation, where ![]() is a (n, 0)-holomorphic form. One further condition is that the Yang–Mills field must satisfy the Donaldson–Uhlenbeck–Yau equation in a torsional background, and the central metaplectic flux compactifications to four dimensions satisfy all conditions above.
is a (n, 0)-holomorphic form. One further condition is that the Yang–Mills field must satisfy the Donaldson–Uhlenbeck–Yau equation in a torsional background, and the central metaplectic flux compactifications to four dimensions satisfy all conditions above.
In six-dimensional Minkowski space–time, the Picard-spinor satisfies:
and thus the space–time metric will be conformal to a Calabi–Yau two-fold
Start with the compactification of type IIB supergravity to six dimensions in the presence of brane sources. Both tensor fields can be complex as opposed to the heterotic case.
I will show that the most general four-manifold describing the internal dimensions is conformal to a Kähler manifold, in contrast with the heterotic case where the four-manifold must be conformally Calabi–Yau
Type IIB string theory compactified to six dimension
As above, the ten-dimensional type IIB supersymmetry transformations are:
and
![]()
with the ten-dimensional supersymmetry parameter being complex and satisfies the Weyl condition:
![]()
with the configurations space satisfies six-dimensional Poincaré-invariance, with line element:
![]()
Hence, supersymmetric configurations satisfy:
![]()
![]()
and
![]()
with a spinor rescalling
![]()
And so, we have a non-constant warp factor ![]() requiring at least one component of
requiring at least one component of ![]() being non-zero.
being non-zero.
Hence, a decomposition of the ten-dimensional spinor allows us to represent an anti-commuting six-dimensional spinor as a pair of Weyl spinors ![]() obeying the symplectic Majorana–Weyl condition:
obeying the symplectic Majorana–Weyl condition:
![]()
![]()
Given the decomposition of the Lorentz algebra
![]()
a positive chirality spinor decomposes as:
![]()
and for the supersymmetry parameter ![]() this decomposition reduces to:
this decomposition reduces to:
![]()
The decomposition is hence invariant under an ![]() transformation acting on the spinor labels i and j and
transformation acting on the spinor labels i and j and ![]() becomes a ten-dimensional Majorana–Weyl spinor.
becomes a ten-dimensional Majorana–Weyl spinor.
Now let me set:
![]()
and
![]()
and by the above decomposition into the supersymmetry variations,
one gets the result that supersymmetry is preserved if and only if the following conditions hold
![]()
![]()
and
![]()
with the dualized one-form field being:
![]()
hence, from:
![]()
![]()
we can derive:
![]()
where
![]()
holds and
![]()
is a complex function. One then obtains that the covariant derivative on the bilinear spinor takes the following form:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{\nabla _m}\left( {{\eta ^{\dagger i}}{\eta _j}} \right) = \frac{1}{2}{\delta ^i}_j\left( {{g_m}\nu + g_m^ * {\nu ^ * }} \right)\\ = {\delta ^i}_j\left( {{\eta ^{\dagger k}}{\gamma _m}\not \partial {D_{{\eta _k}}} + {\eta ^{\dagger k}}\not \partial D{\gamma _m}{\eta _k}} \right)\\ = 2{\delta ^i}_j{\partial _m}D{\eta ^{\dagger k}}{\eta _k}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f6f6cf8015c4d70c48ddf85fea4b5ead_l3.png)
by solving, one can infer:
![]()
![]() being a normalization constant and
being a normalization constant and ![]() is a constant traceless Hermitian matrix.
is a constant traceless Hermitian matrix.
Thus, we can diagonalize on the SU(2) indices to yield:
![]()
Now, I can renormalize the spinors by defining:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\eta _1} = {\alpha _ + }{\lambda _1}}\\{{\eta _2} = {\alpha _ - }{\lambda _2}}\\{{{\tilde \eta }_1} = {\alpha _ - }{{\tilde \lambda }_1}}\\{{{\tilde \eta }_2} = {\alpha _ + }{{\tilde \lambda }_2}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-11e222a5e6d451b88b261a6c7cf9ecbc_l3.png)
with
![]()
and the normalized spinors obey:
![]()
as well as
![]()
with ![]() a
a ![]() -dependent function. From the last two equalities above, it follows that:
-dependent function. From the last two equalities above, it follows that:
![]()
hence, the above supersymmetry conditions become:
![]()
and
![]()
with the following holding:
![]()
![]()
as well as:
![]()
![]()
which combined, yield the constraint:
![]()
giving us the following:
![]()
![]()
where ![]() is:
is:
![]()
The complex structure of the four-manifold
Now consider
![]()
then, from
![]()
we can derive:
![]()
Hence, I just defined an almost hyper-Kähler structure on the four-manifold
So, with respect to ![]() , we have the (p, q)- forms:
, we have the (p, q)- forms:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\Omega _{mn}} = {{\left( {{J_2} + i{J_1}} \right)}_{mn}},\quad \left( {2,0} \right)}\\{{J_{mn}} = {{\left( {{J_3}} \right)}_{mn}},\quad \left( {1,1} \right)}\\{{{\bar \Omega }_{mn}} = {{\left( {{J_2} + i{J_1}} \right)}_{mn}},\quad \left( {0,2} \right)}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d5bfd500127e1ab7a21fdd2639f955d1_l3.png)
The covariant derivatives of the Hermitian form, ![]() , and the complex 2-form,
, and the complex 2-form, ![]() are now:
are now:
![]()
with
![]()
Hence, it follows that the four-manifold is not only complex, but also Kähler, yet, the manifold is Calabi–Yau if and only if
![]()
and so we have a hyper-Kähler structure
The complex structure allows one to introduce holomorphic and anti-holomorphic coordinates ![]() and set:
and set:
![]()
The Kähler form and the metric are related as:
![]()
entailing:
![]()
applied to:
![]()
![]()
as well as:
![]()
![]()
gives us:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{g_a} = - 2\frac{{{\alpha _ + }}}{{{\alpha _ - }}}{e^{ - i\varphi }}{\partial _a}D}\\{{g_{\bar a}} = - 2\frac{{{\alpha _ - }}}{{{\alpha _ + }}}{e^{ - i\varphi }}{\partial _{\bar a}}D}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e92f59a10f53f51e5cd62fb7219536c2_l3.png)
as well as:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{{\not P}_a} = - 2{{\left( {\frac{{{\alpha _ + }}}{{{\alpha _ - }}}} \right)}^2}{e^{ - 2i\varphi }}{\partial _a}D}\\{{{\not P}_{\bar a}} = - 2{{\left( {\frac{{{\alpha _ - }}}{{{\alpha _ + }}}} \right)}^2}{e^{ - 2i\varphi }}{\partial _{\bar a}}D}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e7631505bc536520e08610cf03fe38c0_l3.png)
thus, we can infer:
![]()
Without loss of generality, consider now the class of solutions:
![]()
with ![]() the R–R 1-form and the second condition entailing
the R–R 1-form and the second condition entailing ![]() . In such backgrounds, the following holds:
. In such backgrounds, the following holds:
![]()
and since the sourceless Bianchi identity for ![]() is:
is:
![]()
we can derive the following:
![]()
where the rescalling of the metric:
![]()
gives us:
![]()
Hence, for:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\varphi = 0}\\\pi \\{{{\tilde g}_{mn}}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ee4ccace93252c98a82c9a01a1c81737_l3.png)
we have a correspondence to the metric of the four-manifold in the string frame and this is the result for NS 5-branes
thus,
![]()
with ![]() the density distribution of the 5-branes.
the density distribution of the 5-branes.
hence, type IIB solution are two copies of analogous six-dimensional heterotic backgrounds and the four-manifold must be conformally Calabi–Yau in the heterotic case.
Informal proof:
take the heterotic dilatino and gravitino supersymmetry constraints in the string frame:
![]()
![]()
Given that the string frame metric has the form:
![]()
the supersymmetry transformations become:
![]()
![]()
rescalling the internal metric as:
![]()
we get:
![]()
which is deep, as
is necessarily a Calabi–Yau metric and the internal four-manifold is conformally Calabi–Yau