![]()
![]()
![]()
![]()
with the M5-brane action in a D = 11 SUGRA background is given as such:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=2\int_{{{{M}_{6}}}}{{d{{x}^{6}}}}\left[ {\sqrt{{-\det \left( {{{g}_{{\mu \nu }}}+i{{{\tilde{H}}}_{{\mu \nu }}}} \right)}}} \right.\\+\frac{{\sqrt{{-g}}}}{{4{{{\left( {\partial a} \right)}}^{2}}}}{{\partial }_{\lambda }}a{{{\tilde{H}}}^{{\lambda \mu \nu }}}\left. {{{H}_{{\mu \nu \rho }}}{{\partial }^{\rho }}_{a}} \right]-\int_{{{{M}_{6}}}}{{{{C}_{6}}}}+{{H}_{3}}\wedge {{C}_{3}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f2a7df4d5552e0c092ce01b23b22cfbe_l3.png)
where:
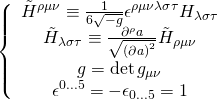
and the ![]() -brane action takes the following form:
-brane action takes the following form:
![]()
where:
![]()
with:
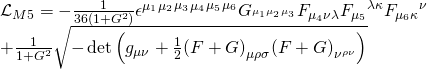
and where the Hamiltonian metaplectic action in the Heisenberg representation yields:
![]()
where:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\Im _i} = - \not \partial {\phi _{si}}{T_{Dp}}d\,\Omega {{({\phi _{si}})}^{2\pi ik}}}\\{\not K = - {{\not \partial }_i}{{\widetilde E}^i} + {{( - 1)}^{p + 1}}{T_{Dp}}{S^{{\rm{Fer}}}}}\\{{{\not H}_i} = \widetilde P{\alpha _i}\widetilde E_i^\alpha {{\not \partial }_i}{\phi _{si}} + \widetilde E{{\not F}_{ij}}}\\{H = \frac{1}{{2\pi ik}}\left[ {{{\widetilde P}^2} + {{\widetilde E}^i}{{\widetilde E}^j}{G_{ij}} + T_{Dp}^2{e^{ - 2{\phi _{si}}}}{\rm{det}}\left( {{G_{ij}} + {{\not F}_{ij}}} \right)} \right]}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bd828556ea51b8c78862eb753658693f_l3.png)
with:
![]()
and:
![]()
where the Ramond-Ramond gauge-coupling sector is given by the following action:
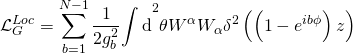
and the action of a ![]() -brane is given by a Dirac-Born-Infeld part coupled to a Chern-Simons WZ part:
-brane is given by a Dirac-Born-Infeld part coupled to a Chern-Simons WZ part:
![]()
with:
![]()
![]()
where ![]() is the worldvolume pullback with
is the worldvolume pullback with ![]() -orientifold action:
-orientifold action:
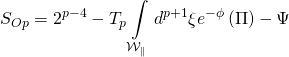
with:
![]()
and
![]()
where the pullback to the ![]() -worldvolume yields the 10-D SYM action:
-worldvolume yields the 10-D SYM action:
![]()
with string coupling:
![]()
and the 10-D SUGRA dimensionally-reduced Type-IIB action is given as such:
![]()
with:
![]()
![]()
![]()
In the string-frame, the type-IIB SUGRA action is given by:
![]()
with:
![]()
![]()
![]()
where the superpotential is given by:
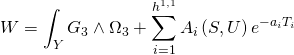
where:
![]()
is the Gukov-Vafa-Witten superpotential stabilization complex term, as well as the axio-dilaton field:
![]()
Given the presence of ![]() -brane instantons,
-brane instantons, ![]() are of Kähler moduli Type-IIB-orbifold class:
are of Kähler moduli Type-IIB-orbifold class:
![]()
with ![]() being the volume of the divisor
being the volume of the divisor ![]() and
and ![]() the 4-form Ramond-Ramond axion field corresponding to:
the 4-form Ramond-Ramond axion field corresponding to:
![]()
and:
![]()
where ![]() is the Kähler form:
is the Kähler form:
![]()
and:
![]()
an integral-form basis and ![]() the associated intersection coefficients. Hence, the desired Kähler potential is given as such:
the associated intersection coefficients. Hence, the desired Kähler potential is given as such:
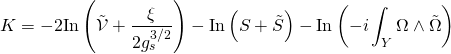
with ![]() the Calabi-Yau volume, and in the Einstein frame, has the following form:
the Calabi-Yau volume, and in the Einstein frame, has the following form:
![]()
The ![]() -term is given by:
-term is given by:
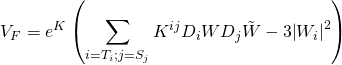
with the large volume scenario ![]() -term given as such:
-term given as such:
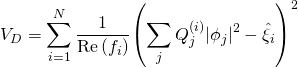
with:
![]()
and the Fayet-Illopoulos terms being:
![]()
where ![]() are the
are the ![]() -brane charge-vectors. Then we saw that the Chern-Simons orientifold action gets a Calabi-Yau curvature correction in the form of:
-brane charge-vectors. Then we saw that the Chern-Simons orientifold action gets a Calabi-Yau curvature correction in the form of:
![Rendered by QuickLaTeX.com \displaystyle {{S}_{{{{O}_{p}},CS}}}=-{{2}^{{p-4}}}-{{T}_{p}}\int\limits_{{{{\mathcal{W}}^{\prime }}}}{{P\left[ C \right]}}\wedge \Theta](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-371c7b529216d796ebd4b8241427e1d1_l3.png)
with
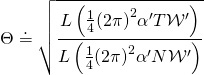
due to the Gauss–Codazzi equations:
![]()
and the Ramond-Ramond term being:
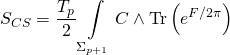
which yields the Type-IIB Calabi-Yau three-fold superpotential:
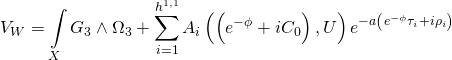
with the topologically mixed Yang-Mills action taking the following form:
![]()
with the corresponding Chern-Simons action:
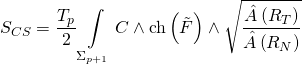
It follows that the equation of motion for an M5-brane, in the abelian case, is given as such:
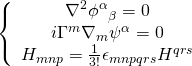
with:
![Rendered by QuickLaTeX.com \displaystyle \left\{ {\begin{array}{*{20}{c}} {{{H}_{{mnp}}}=3{{\partial }_{{\left[ m \right.}}}{{B}_{{\left. {np} \right]}}}} \\ {{{\epsilon }^{{012345}}}=1} \\ {\alpha ,\beta =1,...,4:\quad \text{ind}\left[ {\text{irre}{{\text{p}}^{{fun}}}USp(4)/\text{R-sym}} \right]} \end{array}} \right.](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-268e2455875144b107733e5e2897994a_l3.png)
and are clearly invariant under SUSY transformations:
![Rendered by QuickLaTeX.com \displaystyle \left\{ {\begin{array}{*{20}{c}} {\delta {{\phi }^{{\alpha \beta }}}=-i{{{\bar{\epsilon }}}^{{\left[ \alpha \right.}}}{{\psi }^{{\left. \beta \right]}}}} \\ {\delta {{B}_{{mn}}}=-i{{{\bar{\epsilon }}}^{\alpha }}{{\Gamma }_{{mn}}}{{\psi }_{\alpha }}} \\ {\delta {{\psi }^{\alpha }}={{\nabla }_{m}}{{\phi }^{\alpha }}_{\beta }{{\Gamma }^{m}}{{\epsilon }^{\beta }}+\frac{1}{{2\cdot 3!}}{{\Gamma }^{{mnp}}}{{H}_{{mnp}}}{{\epsilon }^{\alpha }}} \end{array}} \right.](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f22be97caaacf8a5ab4f3d5074c76fa6_l3.png)
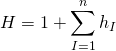
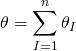
the worldvolume metric is hence given by:
![]()
and asymptotes as such:
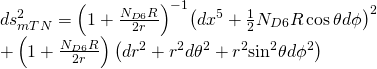
Now, in light of the self-duality of the curvature form, a Killing spinor ![]() satisfying:
satisfying:
exists. Since the bosonic solutions to the Euler-Lagrange equations preserve eight supersymmetries, we have the following relation:
In light-cone gauge, we hence have:
Thus, the Euler-Lagrange equations satisfying eight supersymmetries are:
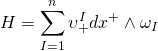
On the multi-centered Taub-NUT space, the 2-form is given as such:
with:
Hence, the fermionic Euler-Lagrange equations are given by:
The energy-momentum tensor for scalars and fermions is given as such:
with the super-Poincaré operator given by:
Hence, the abelian conserved current takes the following form:
for all 1-forms derived from the gauge symmetry corresponding to the Hermitian Yang-Mills equations, with total charge:
Restricting to ![]() , asymptotically we get:
, asymptotically we get:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}Q\left( {{{\Lambda }_{5}}\left( \infty \right)} \right)=\frac{1}{{2\pi R}}\text{Tr}\sum\limits_{I}{{\oint_{{\mathbb{R}\times {{S}^{1}}\times S_{\infty }^{2}}}{{d{{\Omega }_{2}}}}}}d{{x}^{+}}\left[ {H{{\partial }_{r}}} \right.\left( {\frac{{{{h}_{I}}}}{H}} \right)+\\{{\varepsilon }^{{rjk}}}{{\theta }_{j}}{{\partial }_{k}}\left. {\left( {\frac{{{{h}_{I}}}}{H}} \right)} \right]\upsilon _{+}^{I}{{\Lambda }_{5}}\left( \infty \right)\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-3341bd214a5cf26faf8f53a58abcc3e2_l3.png)
and where the D4-brane ![]() gauge field is given as such:
gauge field is given as such:
In the non-abelian case, the M5-brane compactified on a circle of radius R yields at low energy a 5D M-SYM. An elliptic multi-centered Taub-NUT reduction on ![]() imposes the following metric:
imposes the following metric:
with Yang-Mills action:
and the scalar action:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{S}_{s}}^{\phi }=-\frac{1}{{8{{\pi }^{2}}R}}\text{tr}\int{{{{d}^{5}}}}x\sqrt{{-g}}\left( {\sqrt{H}} \right.{{D}_{\mu }}{{\phi }_{{\alpha \beta }}}{{D}^{\mu }}{{\phi }^{{\alpha \beta }}}+\\\frac{1}{4}\frac{1}{{{{H}^{{5/2}}}}}{{\partial }_{i}}H{{\partial }_{i}}H{{\phi }_{{\alpha \beta }}}{{\phi }^{{\alpha \beta }}}-\sqrt{H}\left[ {{{\phi }^{{\alpha \beta }}},\left. {{{\phi }_{\beta }}^{\delta }} \right]} \right.\left. {\left[ {{{\phi }_{{\delta \gamma }}},{{\phi }^{\gamma }}_{\alpha }} \right]} \right)\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-454b7a969ebf35a2e16ca01028a7062a_l3.png)
and our Chern-Simons term is hence given by:
We can now analyze the M5-brane from the perspective of the D3/D5-brane configuration system. The Killing spinor equation in such a system is given as such:
with SUSY-variation:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\delta {{\psi }^{\alpha }}=\frac{1}{2}{{F}_{{\mu \nu }}}{{\gamma }^{{\mu \nu }}}{{\varepsilon }^{\alpha }}+2i\sqrt{H}{{M}_{{\beta \gamma }}}{{D}_{\mu }}\left( {\frac{1}{{\sqrt{H}}}{{\phi }^{{\alpha \beta }}}} \right){{\gamma }^{\mu }}{{\varepsilon }^{\gamma }}\\-\frac{1}{{\sqrt{H}}}{{M}_{{\beta \gamma }}}{{\phi }^{{\alpha \beta }}}{{{\tilde{F}}}_{{\mu \nu }}}{{\gamma }^{{\mu \nu }}}{{\varepsilon }^{\gamma }}+2{{M}_{{\beta \gamma }}}{{M}_{{\delta \lambda }}}\left[ {{{\phi }^{{\alpha \beta }}},{{\phi }^{{\gamma \delta }}}} \right]{{\varepsilon }^{\gamma }}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1f65ecec3c413acb33f0dcef16ee2d23_l3.png)
and field strength:
The covariant derivative is hence given in terms of a field transforming in the adjoint representation of the gauge group:
and the BPS conditions are given by:
Hence, we can derive:
![Rendered by QuickLaTeX.com \displaystyle \left\{ {\begin{array}{*{20}{c}} {{{D}_{i}}\left( {\sqrt{H}{{\phi }^{\alpha }}_{\beta }} \right)={{D}_{-}}{{\phi }^{\alpha }}_{\beta }=0} \\ {{{{\left[ {{{\phi }^{\alpha }}_{\beta },{{\phi }^{\beta }}_{\gamma }} \right]}}_{\mathfrak{g}}}=0} \end{array}} \right.](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-7dd43891557f8a5af3c02c6193c82685_l3.png)
from which the Euler-Lagrange equations follow as such:
In light of the BPS conditions:
it follows that, up to metaplecticomorphism, solutions to the BPS equation are gauge transformations of configuration type:
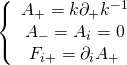
Hence, the Euler-Lagrange equations are given by:
with:
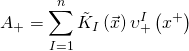
Our Yang-Mills form is thus given by:
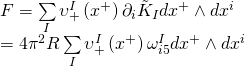
Hence, ![]() becomes an element of the full M5-brane gauge algebra given that the following identity holds:
becomes an element of the full M5-brane gauge algebra given that the following identity holds:
The fermionic Euler-Lagrange equation is given by:
the second being the Dirac equation for:
and the D-term in the first equation is the only source of the non-abelian gauge field. Hence we have, in terms of a representation highest weight term member ![]() , the following equation:
, the following equation:
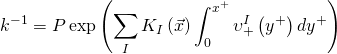
Consequently, the following can be derived:
The energy-momentum tensor is thus given as such:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{T}_{{\mu \nu }}}=\frac{1}{{8{{\pi }^{2}}R}}\text{tr}\left[ {2\sqrt{H}} \right.{{D}_{\mu }}{{\phi }_{{\alpha \beta }}}{{D}_{\nu }}{{\phi }^{{\alpha \beta }}}+\\\frac{1}{{2{{H}^{{3/2}}}}}{{\partial }_{\mu }}H{{\partial }_{\nu }}H{{\phi }_{{\alpha \beta }}}{{\phi }^{{\alpha \beta }}}+2\sqrt{H}{{F}_{{\mu \rho }}}{{F}_{\nu }}^{\rho }\\-{{g}_{{\mu \nu }}}\left( {2\sqrt{H}{{D}_{\rho }}{{\phi }_{{\alpha \beta }}}{{D}^{\rho }}{{\phi }^{{\alpha \beta }}}+} \right.\frac{1}{4}\frac{1}{{{{H}^{{5/2}}}}}{{\partial }_{i}}H{{\partial }_{i}}H{{\phi }_{{\alpha \beta }}}{{\phi }^{{\alpha \beta }}}\\+\frac{{\sqrt{H}}}{2}{{F}_{{\rho \sigma }}}{{F}^{{\rho \sigma }}}-\sqrt{H}\left[ {{{\phi }^{{\alpha \beta }}},{{\phi }_{{\beta \lambda }}}} \right]\left. {\left. {\left[ {{{\phi }^{{\lambda \rho }}},{{\phi }_{{\rho \alpha }}}} \right]} \right)} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-b78f9fcf432bd6d015989b35fc46bf30_l3.png)
and entails:
and so the energy-momentum tensor reduces to the following form:
giving us the spacial integral relation:
corresponding to ![]() copies of multi-centered Taub-NUT spaces of a Wess–Zumino–Witten–Novikov model for each
copies of multi-centered Taub-NUT spaces of a Wess–Zumino–Witten–Novikov model for each ![]() , and crucially, the non-abelian gauge charges for our M5-brane action take the following form:
, and crucially, the non-abelian gauge charges for our M5-brane action take the following form:
with corresponding charges:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c}Q\left( {\Lambda \left( \infty \right)} \right)=\frac{1}{{4{{\pi }^{2}}R}}\text{tr}\sum\limits_{I}{{\oint{{d{{\Omega }_{2}}}}}}d{{x}^{+}}\left[ {H{{\partial }_{r}}} \right.{{K}_{I}}+\\{{\varepsilon }^{{rjk}}}\left. {{{\theta }_{j}}{{\partial }_{k}}{{K}_{I}}} \right]\upsilon _{+}^{I}\Lambda \left( \infty \right)=-\frac{1}{{2\pi }}\text{tr}\sum\limits_{I}{{{{N}_{I}}}}\int{{d{{x}^{+}}}}\upsilon _{+}^{I}\Lambda \left( \infty \right)\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-167cc1730b944161e3c9994027137c59_l3.png)
Thus, the action of our BPS sector yields the desired result: a Wess–Zumino–Witten–Novikov model for a multi-centered Taub-NUT space directly arising from M-theory: