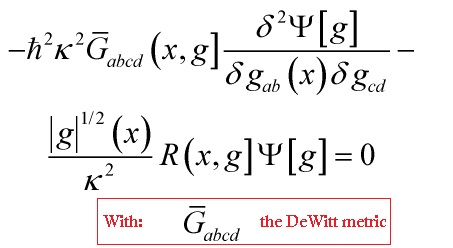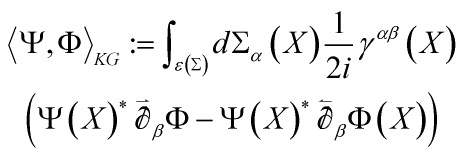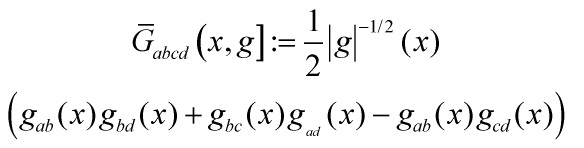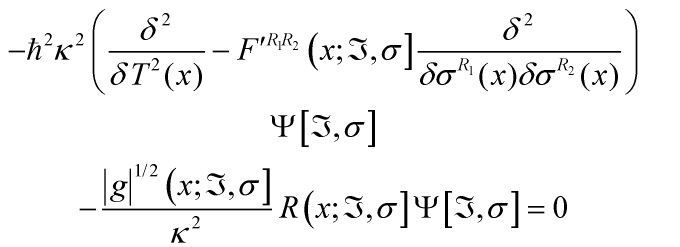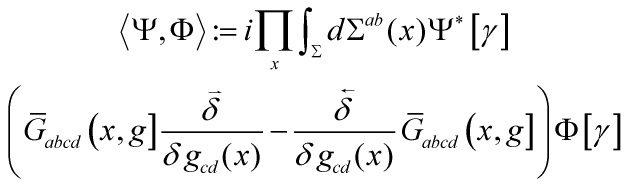Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

On the Klein-Gordon ‘Hilbert-Space-Problem’ of Time

By Posted on In Cosmology, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Time ,
photo

Given, as I showed, that the Eulerian fluid action, after the ADM splitting, is

    \[{S_F}\int_\mathbb{R} {dt} \int_\sigma {{d^3}} x\sqrt q N{\rho _0}\left( {\sqrt {\left( {{v_\mu }{n^\mu }} \right) - {v_a}{v^a}} - TS} \right)\]

with

    \[\left\{ {\begin{array}{*{20}{c}}{{\chi _1} = {p_\alpha } = 0}\\{{\chi _2} = {p_\beta } - \alpha \pi = 0}\\{{\chi _3} = {p_\theta } = 0}\\{{\chi _4} = {p_S} - \theta \pi }\end{array}} \right.\]

the entropy S, given the Mandelstam-Tamm formulation of a time-energy uncertainty relation, entails the undefinability of inner products of functional differential operators for this form of the Wheeler-DeWitt equation:

 

eq1

 

and at face value, that is a no-go theorem for the ‘existence’ of time outside of string-theory’s AdS/CFT duality, but not to be addressed here. Let me ignore the operator-ordering problem to reduce the WdW-equation to

    \[\left( {{\hbar ^2}{e^{ - 3\Omega }}\left( {\frac{1}{{24}}\frac{{{{\not \partial }^2}}}{{\not \partial {\Omega ^2}}} - \frac{1}{2}\frac{{{{\not \partial }^2}}}{{\not \partial {\phi ^2}}}} \right) - 6k{e^\Omega } + {e^{3\Omega }}V(\phi )} \right)\psi \left( {\Omega ,\phi } \right) = 0\]

and try and define an inner product via the Klein-Gordon interpretation of quantum gravitational geometrodynamics and proceed from there. In this section, I will lead us to a rather foundationally deep problem for time, namely: the Hilbert-Space-Problem. Let’s start with the issue of interpreting the WdW-equation, with chiefly two main philosophically and mathematically acute issues: defining an inner product and how to extract a notion of time evolution from the Wheeler-DeWitt equation. One inner-product immediately, for scalar reasons, suggests itself:

    \[\left\langle {\Psi \left| \Phi \right.} \right\rangle : = \int_{{\rm{Riem}}\left( \Sigma \right)} {Dg{\Psi ^ * }} \left[ g \right]\Phi \left[ g \right]\]

this is the Schrödinger IP-interpretation. Let me draw a parallel between the Wheeler-DeWitt equation

    \[\left( {{\hbar ^2}{e^{ - 3\Omega }}\left( {\frac{1}{{24}}\frac{{{{\not \partial }^2}}}{{\not \partial {\Omega ^2}}} - \frac{1}{2}\frac{{{{\not \partial }^2}}}{{\not \partial {\phi ^2}}}} \right) - 6k{e^\Omega } + {e^{3\Omega }}V(\phi )} \right)\psi \left( {\Omega ,\phi } \right) = 0\]

and the Klein-Gordon equation of a ‘particle’ moving in a curved space with an arbitrary, time-dependent potential which is valid in the minisuperspace model. So, take a relativistic particle of mass M moving in a four-dimensional spacetime \left( {M,\gamma } \right) where \gamma is a rigid Lorentzian metric. Classically, the trajectories of the particle in M are parametrised by an arbitrary real number \tau and the theory is invariant under the reparametrisation \tau \to \tau '\left( \tau \right). Note, this invariance leads to the constraint H\left( {X,P} \right) = 0 and the superHamiltonian

    \[H\left( {X,P} \right): = \frac{1}{{2M}}{\gamma ^{\alpha \beta }}\left( X \right){P_\alpha }{P_\beta } + V\left( X \right)\]

This constraint becomes the Klein-Gordon equation in the quantum theory:

    \[\left( {{\gamma ^{\alpha \beta }}\left( X \right){\nabla _\alpha }{\nabla _\beta } + V\left( X \right)} \right)\Psi \left( X \right) = 0\]

Here is the deep point, any interpretation of this equation is based on the pairing between any pair of solutions 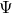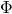\Psi, \Phi defined by

 

eq1

 

and the integral is taken over the hypersurface \varepsilon \left( \Sigma \right) of M defined by an embedding \varepsilon :\Sigma \to M that is spacelike with respect to the background metric \gamma, with crucially:

    \[d{\Sigma _\alpha }\left( X \right): = {\varepsilon '_{\alpha \beta \gamma \delta }}d{X^\beta } \wedge d{X^\gamma } \wedge d{X^\delta }\]

Hence, the Klein-Gordon equation entails that {\left\langle {\Psi ,\Phi } \right\rangle _{KG}} is independent of \varepsilon, thus {\left\langle {\Psi ,\Phi } \right\rangle _{KG}} is the right choice for a scalar product. Yet, we have a problem, since it is not positive-definite:

    \[{\left\langle {\Psi ,\Psi } \right\rangle _{KG}} = 0\]

holds for all real functions \Psi, and complex solutions to the Klein-Gordon equation exist for which {\left\langle {\Psi ,\Psi } \right\rangle _{KG}} < 0.

A classic resolution is looking for a timelike vector field U that is a Killing vector for the spacetime metric and is also such that the potential is constant along its flow lines. A choice of time function is naturally \tau \left( X \right) and is the parameter along these flow lines, defined as a solution to the partial differential equation:

    \[{U^\alpha }\left( X \right){\not \partial _\alpha }\tau \left( X \right) = 1\]

it follows that the energy

    \[E\left( {X,P} \right) = - {P_\tau }: = - {U^\alpha }\left( X \right){P_\alpha }\]

of the particle is a constant of the motion with \left\{ {E,H} \right\} = 0. Now, upon quantisation, we get

    \[\left[ {\hat E,\hat H} \right] = 0\]

such that if all the operators are self-adjoint with respect to the inner product

    \[\left\langle {\Psi \left| \Phi \right.} \right\rangle : = \int_{{\rm{Riem}}\left( \Sigma \right)} {Dg{\Psi ^ * }} \left[ g \right]\Phi \left[ g \right]\]

it would mean it is possible to find simultaneous eigenstates of

    \[\hat E: = i\hbar {U^\alpha }{\not \partial _\alpha }\]

and

    \[H\left( {X,P} \right): = \frac{1}{{2M}}{\gamma ^{\alpha \beta }}\left( X \right){P_\alpha }{P_\beta } + V\left( X \right)\]

Thus it makes sense to select those solutions of the Klein-Gordon equation that have positive energy, and one can see that the inner product

 

eq1

 

is positive on such solutions. On such a class of solutions, and this is key, the Klein-Gordon equation is equivalent to the standard Schrödinger equation using the above chosen time parameter.

In applying these ideas to the Wheeler-DeWitt equation

the key is that the DeWitt metric

 

eq2

 

 

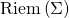on {\rm{Riem}}\left( \Sigma \right) has a hyperbolic character in which the conformal modes of the metric play the role of time-like direction

which entails that it is possible to choose an internal time functional \Im \left( {x,g} \right] so that the Wheeler-DeWitt equation takes the following form:

 

eq3

 

with {\sigma ^R}\left( {x,g} \right], R = 1, . . ., 5 denoting the 5 \times {\infty ^3} modes of the metric variables {g_{ab}}(x) that remain after identifying the 1 \times {\infty ^3} internal time modes \Im (x).

So, we start with the formal pairing analogue of the point-particle expression:

eq1

 

and get:

 

eq4

 

between solutions \Psi and \Phi of the Wheeler-DeWitt equation and in the minisuperspace setting, the Wheeler-DeWitt equation:

    \[\left( {{\hbar ^2}{e^{ - 3\Omega }}\left( {\frac{1}{{24}}\frac{{{{\not \partial }^2}}}{{\not \partial {\Omega ^2}}} - \frac{1}{2}\frac{{{{\not \partial }^2}}}{{\not \partial {\phi ^2}}}} \right) - 6k{e^\Omega } + {e^{3\Omega }}V(\phi )} \right)\psi \left( {\Omega ,\phi } \right) = 0\]

simplifies due to multiplication of both sides by

    \[{e^{3\Omega }}\]

to yield:

    \[\left( {{\hbar ^2}\left( {\frac{1}{{24}}\frac{{{{\not \partial }^2}}}{{\not \partial {\Omega ^2}}} - \frac{1}{2}\frac{{{{\not \partial }^2}}}{{\not \partial {\phi ^2}}}} \right) - 6\kappa {e^{4\Omega }} + {e^{6\Omega }}V(\phi )} \right)\psi \left( {\Omega ,\phi } \right) = 0\]

with the corresponding scalar product

    \[\left\langle {\psi ,\phi } \right\rangle : = i\int_{\Omega = {\rm{const}}} {d\phi } \left( {{\psi ^ * }\frac{{\not \partial \phi }}{{\not \partial \Omega }} - \phi \frac{{\not \partial {\psi ^ * }}}{{\not \partial \Omega }}} \right)\]

which is conserved in \Omega-time by virtue of:

    \[\left( {{\hbar ^2}\left( {\frac{1}{{24}}\frac{{{{\not \partial }^2}}}{{\not \partial {\Omega ^2}}} - \frac{1}{2}\frac{{{{\not \partial }^2}}}{{\not \partial {\phi ^2}}}} \right) - 6\kappa {e^{4\Omega }} + {e^{6\Omega }}V(\phi )} \right)\psi \left( {\Omega ,\phi } \right) = 0\]

Things look good until one realizes that the right hand side of:

 

eq4

 

cannot serve as a Hilbert space inner product since it is not positive definite as in the point-particle scenario, and thus it is not possible to define physical states as an analogue of the positive-frequency solutions of the normal Klein-Gordon equation, and so there can be no selection of an intrinsic time functional \Im \left( {x,g} \right], hence, the non-existence of a suitable Killing vector on {\rm{Riem}}\left( \Sigma \right) follows: this is the ‘Hilbert space problem’ for time

Untitled

previously

S-Duality, Entropy and the Problem of Time in Quantum Physics

up next

Can a Dirac-Schrödinger 'Quantum Space Analysis' Solve the Problem of Time Scale-Invariantly?!
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on