The importance of D3-branes derives partly from their role in F-theory due to D3/D7-brane systems in the presence of orientifolds, yielding an effective 4D N = 1 F-action, and D3-branes naturally correspond to M5-branes in M-theory compactified on a Type-II-A/B torus, and instantons that arise from D3-branes wrapping internal divisors on a Calabi-Yau 3-fold correspond to M5-brane instantons in M-theory compactified on an elliptically fibered Calabi-Yau 4-fold. Moreover, a unique property of D3-branes is self-duality. Hence, for the M5-![]() algebra to close, the D3 worldvolume super-Hamiltonian must exhibit manifest Poincaré symmetry. Note that Dp-brane solutions, for p = 1, 2, 3, 4, preserving 1/2 SUSY, have general form:
algebra to close, the D3 worldvolume super-Hamiltonian must exhibit manifest Poincaré symmetry. Note that Dp-brane solutions, for p = 1, 2, 3, 4, preserving 1/2 SUSY, have general form:
![]()
![]()
![]()
![]()
where the M5-brane action in a D = 11 SUGRA background is given by:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=2\int_{{{{M}_{6}}}}{{d{{x}^{6}}}}\left[ {\sqrt{{-\det \left( {{{g}_{{\mu \nu }}}+i{{{\tilde{H}}}_{{\mu \nu }}}} \right)}}} \right.\\+\frac{{\sqrt{{-g}}}}{{4{{{\left( {\partial a} \right)}}^{2}}}}{{\partial }_{\lambda }}a{{{\tilde{H}}}^{{\lambda \mu \nu }}}\left. {{{H}_{{\mu \nu \rho }}}{{\partial }^{\rho }}_{a}} \right]-\int_{{{{M}_{6}}}}{{{{C}_{6}}}}+{{H}_{3}}\wedge {{C}_{3}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f2a7df4d5552e0c092ce01b23b22cfbe_l3.png)
with:
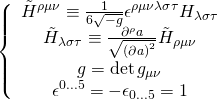
and the ![]() -brane action takes the following form:
-brane action takes the following form:
![]()
where:
![]()
with:
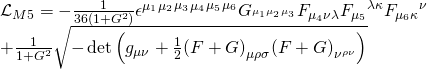
Now, a D3-brane has a super-Yang-Mills worldvolume theory and at strong coupling, it constitutes a black brane solution of type II supergravity. Hence, by D3 self-duality, the bosonic D3-brane action with a super-Lagrangian coupling is given by:
![Rendered by QuickLaTeX.com \[{S_{D3}} = \frac{1}{{4{k^2}{C_{\left[ 4 \right]}}}}\int {\sqrt {\widetilde {{k_{\mu \nu }}^{ - 2\Phi }}} } \left( {2{k^{\mu \nu }}{C_{\left[ 2 \right]}} + \frac{\lambda }{8} + {{\partial }_\mu }\Phi \,\partial _\phi ^\mu \Phi - C_{\left[ 4 \right]}^\Phi - 1{K_{\mu \nu }}^{ * \dagger }} \right){L_{G(D3)}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6d1159e1ff5a5ff73d342ba4a336ec46_l3.png)
with:
![]()
and where the Ramond-Ramond gauge-coupling sector is given by the action:
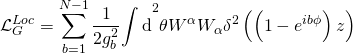
and the Ramond-Ramond term being:
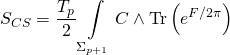
which yields the Type-IIB Calabi-Yau three-fold superpotential:
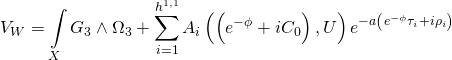
and where the topologically mixed Yang-Mills action is given by:
![]()
with the corresponding Chern-Simons action:
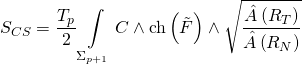
and where the Ramond-Ramond coupling-term:
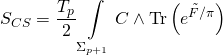
has variational action:
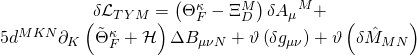
However, one must exhibit the self-duality of the D3-brane in the Hamiltonian metaplectic setting in order for the M5-![]() algebra to close. To that end, I will derive that as well as the induced D-brane and M5-brane Hamiltonians. First we note that one can always lift an
algebra to close. To that end, I will derive that as well as the induced D-brane and M5-brane Hamiltonians. First we note that one can always lift an ![]() duality to an
duality to an ![]() duality by introducing the D3-brane dilaton
duality by introducing the D3-brane dilaton ![]() and axion
and axion ![]() which are constant background fields. Then, we can re-define an
which are constant background fields. Then, we can re-define an ![]() -dual Lagrangian as such:
-dual Lagrangian as such:
![]()
with ![]() . From the above
. From the above ![]() -dual Lagrangian, the D3-brane Hamiltonian action can be derived as:
-dual Lagrangian, the D3-brane Hamiltonian action can be derived as:
![]()
where:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{L^{DBI}} = - \sqrt { - {\rm{det}}\left( {{G_{\mu \nu }} + {F_{\mu \nu }}} \right)} }\\{{G_{\mu \nu }} = \prod _\mu ^M{\prod _\mu }M}\\{{F_{\mu \nu }} = {{\partial }_{\left[ {\mu A\nu } \right]}} + \Omega _{\mu \nu }^3}\\{\Omega _{\mu \nu }^i = {{\widetilde {\theta {{\prod }_{{{\left[ {\mu {\tau _j}{{\partial }_\nu }} \right]}^\theta }}}}}^{ * \dagger }}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f3a24033705522c718c9674ab3579aa4_l3.png)
![]() and
and ![]() are the Pauli matrices cohomologically acting on the supersymmetric group indices, and
are the Pauli matrices cohomologically acting on the supersymmetric group indices, and ![]() is the Wess-Zumino Lagrangian satisfying the Matsubara condition, and is given by:
is the Wess-Zumino Lagrangian satisfying the Matsubara condition, and is given by:
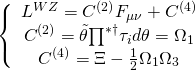
where ![]() and
and ![]() are the RR-2 and RR-4 forms, and
are the RR-2 and RR-4 forms, and ![]() represents the Kappa symmetry of the gauge bundle of the D3-brane’s
represents the Kappa symmetry of the gauge bundle of the D3-brane’s ![]() topology. Now, let:
topology. Now, let:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\left( {{X^M},{P^M}} \right)}\\{\left( {\theta ,\,{\pi _\theta }} \right)}\\{\left( {{A_\mu },{E^\mu }} \right)}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-8ace3f50e2d533f7b52c602e7e0da2e0_l3.png)
be a canonical conjugate set for the super-Kahler phase-space variables, and define the critical 3-dimensional anti-symmetric tensor:
![]()
and introduce the de Rham variables:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{{B}^i} = \frac{1}{2}{\varepsilon ^{ijk}}{F_{ik}} = {e^{ - \Phi /2}}{B^i} + \frac{1}{2}{\varepsilon ^{ijk}}\Omega _{jk}^3}\\{{B^i} = \frac{1}{2}{\varepsilon ^{ijk}}{F_{ij}}\;;\,\;\left( {i,j,k = 1,2,3} \right)}\\{{{P}_M} \equiv \frac{{\partial {L^{DBI}}}}{{\partial \prod _0^M}} = P_M^{ * \dagger } - {e^{\phi /2}}{{\left( {E + \chi B} \right)}^i} \cdot \frac{{\partial {F_{0i}}(\prod ,\widetilde \theta )}}{{\partial \prod _0^M}} - \frac{{\partial {L^{WZ}}\left( {\prod ,F,\widetilde \theta } \right)}}{{\partial \prod _0^M}}}\\{{{\Sigma }^i} \equiv \frac{{\partial {L^{DBI}}}}{{\partial {F_{0i}}}} = {e^{\phi /2}}{{\left( {E + \chi B} \right)}^i} - \frac{{\partial {L^{WZ}}\left( {\prod ,F,\widetilde \theta } \right)}}{{\partial {F_{0i}}}}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5d642203e5bc7eac7b90a3bcd9a95c37_l3.png)
where ![]() transforms as:
transforms as:
![]()
One then finds that the constraints of the system are given by:
– ![]() symmetry constraint
symmetry constraint
– ![]()
– ![]()
– the p + 1 diffeomorphism constraints:
![]()
![]()
as well as:
– the fermionic constraints:
![Rendered by QuickLaTeX.com \[\begin{array}{c}\psi \equiv {\pi _0} - {{P}_M}\frac{{\partial \prod _o^M}}{{\partial \widetilde \theta }} - {e^{\phi /2}}{\left( {E + \chi B} \right)^i}\frac{{\partial {F_{0i}}\left( {\prod ,\widetilde \theta } \right)}}{{\partial \widetilde \theta }}\\ - \frac{{\partial {L^{WZ}}\left( {\prod ,F,\widetilde \theta } \right)}}{{\partial \widetilde \theta }}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-3a21b501027055136380f50770be8634_l3.png)
with ![]() being the spatial part of the
being the spatial part of the ![]() metric, and its determinant being
metric, and its determinant being ![]() . One must now show the Poincaré invariance of the bosonic constraints:
. One must now show the Poincaré invariance of the bosonic constraints:
![]()
and that the supersymmetric covariance of the fermionic constraint ![]() under the
under the ![]() transformation of
transformation of ![]() and
and ![]() corresponding to the
corresponding to the ![]() fermionic field rotation holds. Note that we get:
fermionic field rotation holds. Note that we get:
![]()
and:
![Rendered by QuickLaTeX.com \[{\left( {{\Omega ^l}} \right)^i} \equiv {\varepsilon ^{ijk}}\widetilde \theta \prod _i^{ * \dagger }{\tau _l}\,\partial \theta \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-0e569e0ce747e5c33fc29bfaefef72b8_l3.png)
with ![]() being an
being an ![]() matrix satisfying:
matrix satisfying:
![]()
and transforms as:
![]()
with:
![]()
and
![]()
and ![]() being an
being an ![]() transformation satisfying:
transformation satisfying:
![]()
and:
![]()
with ![]() rotation
rotation ![]() .
.
To establish D3-brane self-duality, we must consider:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{{P}_M} = P - \left( {{{\Sigma }^i}\frac{{\partial {F_{01}}\left( {\prod ,\widetilde \theta } \right)}}{{\partial \prod _0^M}} + {{B}^i}\frac{{\partial C_{ij}^{(2)}\left( {\prod ,\widetilde \theta } \right)}}{{\partial \prod _o^M}}} \right) - \\\left( {\frac{1}{2}{\varepsilon ^{ijk}}C_{ij}^{(2)}\frac{{\partial {F_{0i}}\left( {\prod ,\widetilde \theta } \right)}}{{\partial \prod _0^M}} + \frac{{\partial }}{{\partial \prod _0^m}}\sqrt { - {G_{\mu \nu }}} {C^{(4)}}\left( {\prod ,\widetilde \theta } \right)} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-16703a55592542b3bdce5c15b23a1d2e_l3.png)
while noting that all terms in the above expression as well as ![]() are invariant under Poincaré duality transformations. So,
are invariant under Poincaré duality transformations. So, ![]() , the conjugate of
, the conjugate of ![]() , is also likewise invariant, hence:
, is also likewise invariant, hence:
![]()
reduces to:
![Rendered by QuickLaTeX.com \[\begin{array}{c}\left( {{{\Sigma }^i}\frac{{\partial {F_{0i}}}}{{\partial \prod _0^M}} + \frac{1}{2}{\varepsilon _{ijk}}{{B}^i}\frac{{\partial {C^{{{(2)}^{jk}}}}}}{{\partial \prod _0^M}}} \right) \cdot {{\Sigma }^i}\widetilde {\theta \,}{\Gamma _M}{\tau _3}\,{{\partial }_i}\theta = \left( {{{B}^i},{{\Sigma }^i}} \right) \cdot \\\left( {\begin{array}{*{20}{c}}{\widetilde {\theta \,}{\Gamma _M}{\tau _1}{{\partial }_i}\theta }\\{\widetilde \theta \,{\Gamma _M}{\tau _3}\,\partial \theta }\end{array}} \right) = \widetilde {\theta \,}\Gamma {\tau _{{0^i}}}{{\partial }_i}\widetilde \theta \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f39cd83b879df5895d9b0e2259b040e4_l3.png)
where:
![]()
holds. In terms of differential forms:
![]()
reduces to:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{C^{{{(2)}^{0,i}}}}\frac{{\partial {F_{0i}}}}{{\partial \prod _0^M}} + \frac{{\partial }}{{\partial \prod _0^M}}\sqrt { - {G_{\mu \nu }}} {C^{(4)}} \to \frac{1}{2}{\left[ { - \left( {\widetilde \theta {\Gamma _M}{\tau _{\left[ {3d\theta } \right]}}\,d\theta } \right)\left( {\widetilde \theta \prod {\tau _1}d\theta } \right)} \right]_3} + \\{\left[ {\frac{{\partial {C^{(4)}}}}{{\partial \prod _0^M}}} \right]_3} = \frac{1}{2}{\left[ { - \widetilde {\theta \,}{\Gamma _M}{\tau _{\left[ {3d\theta } \right]}}d\theta \left( {\widetilde \theta \prod {\tau _1}d\theta } \right)} \right]_3} + {\left[ {\frac{{\partial }}{{\partial \prod _0^M}}\left( {{C^{(4)}} + \frac{1}{2}{\Omega _1}\,{\Omega _3}} \right)} \right]_3}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-95982b792581ace9d14087437901e1eb_l3.png)
where ![]() represents a spatial 3-form coefficient of
represents a spatial 3-form coefficient of ![]() , and given the Poincaré invariance of
, and given the Poincaré invariance of ![]() and
and ![]() under
under ![]() rotation, one can finish the proof by utilizing the gauge invariance of
rotation, one can finish the proof by utilizing the gauge invariance of ![]() and by using the identity:
and by using the identity:
![]()
Diffeomophically, ![]() and
and ![]() essentially appear in the irreducible representation of
essentially appear in the irreducible representation of ![]() , and thus,
, and thus, ![]() and
and ![]() also have Poincaré invariance. Now, the supersymmetric covariance of the fermionic constraints with the above
also have Poincaré invariance. Now, the supersymmetric covariance of the fermionic constraints with the above ![]() is:
is:
![Rendered by QuickLaTeX.com \[\begin{array}{c}\psi = {\pi _\theta } + {{P}_M}\left( {\widetilde \theta \,{\Gamma ^M}} \right) - \left( {{{\Sigma }^i}\frac{{\partial {F_{0i}}}}{{\partial \widetilde \theta }} + \frac{1}{2}{\varepsilon _{ijk}}{{B}^i}\frac{{\partial {C^{{{(2)}^i}}}}}{{\partial \widetilde \theta }}} \right) - \\\left( {{C^{{{(2)}^{0i}}}}\frac{{\partial {F_{0i}}}}{{\partial \widetilde \theta }} + \frac{{\partial \sqrt { - {G_{\mu \nu }}} {C^{(4)}}}}{{\partial \widetilde \theta }}} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-480db143aaf04ae1dfbbae5d90e31c86_l3.png)
where one finds by Gaussian functional reduction:
![Rendered by QuickLaTeX.com \[\left( {{{\Sigma }^i}\frac{{\partial {F_{0i}}}}{{\partial \widetilde \theta }} + \frac{1}{2}{\varepsilon _{ijk}}{{B}^i}\frac{{\partial {C^{{{(2)}^{jk}}}}}}{{\partial \widetilde \theta }}} \right) = \frac{1}{2}\widetilde {\theta \,}{\Gamma _{\tau _0^i}}{\partial _i}\theta \cdot \widetilde \theta \,\Gamma - \widetilde {\theta \,}{\Gamma _{\tau _0^i}}{\prod _i}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-fd0b28ed2fcdff11dbbcd7ef027a4f4b_l3.png)
and:
![]()
Now, given that ![]() transforms as:
transforms as:
![]()
where ![]() is the D3-brane tension, the fermionic expression
is the D3-brane tension, the fermionic expression ![]() covariantly transforms as:
covariantly transforms as:
![]()
Now we must exhibit the self-duality of the D3-brane Hamiltonian, given the gauge field, as usual, ![]() , acting on the automorphic group of
, acting on the automorphic group of ![]() , and the D = 3 metric
, and the D = 3 metric ![]() replaced by the D3-brane worldvolume 4-D metric
replaced by the D3-brane worldvolume 4-D metric ![]() , expressed in terms of brane coordinates
, expressed in terms of brane coordinates ![]() . Note that for any function
. Note that for any function ![]() on the super-Kähler phase-space, we have:
on the super-Kähler phase-space, we have:
![]()
with:
![Rendered by QuickLaTeX.com \[W = \lambda \int {{d^3}} \sigma \sqrt {\gamma _{ij}^{D3}} \left[ {\frac{1}{2}\frac{{\Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }}D_{il}^{ - 1}\frac{{\Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }} + \frac{1}{2}{A_i}{D^{ij}} + {\pi _\theta }\frac{{i{\tau _2}}}{2}\theta } \right]\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ed4801434948ed0105c1ea242e8f627f_l3.png)
where ![]() is a tensor acting on a vector as such:
is a tensor acting on a vector as such:
![]()
with:
![]()
being the covariant anti-symmetric constant tensor, and is the inverse of:
![]()
In the projective geometry of ![]() , we then have:
, we then have:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{D_{im}^{ - 1}{D^{mk}} = {\rm O}_i^k(\nabla )}\\{{\rm O}_i^k(\nabla ) = \delta _i^k - {\nabla _i}({\Delta ^{ - 1}}){\nabla ^k}}\\{{D^{im}}D_{mk}^{ - 1} = {\rm O}_k^i(\nabla )}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-fba056972abdf3d7134d5b89681760a8_l3.png)
noting that ![]() longitudinally projects out the components of the covariant derivative
longitudinally projects out the components of the covariant derivative ![]() .
.
Now, in the D3-brane 4-dimensional curved worldspace, the Laplacian operator ![]() is given by:
is given by:
![]()
with ![]() being the Ricci tensor. One then derives, by use of the Atiyah–Singer index theorem, the fact that
being the Ricci tensor. One then derives, by use of the Atiyah–Singer index theorem, the fact that ![]() generates the desired
generates the desired ![]() duality transformation for the gauge field, and generates the
duality transformation for the gauge field, and generates the ![]() rotation of
rotation of ![]() :
:
![Rendered by QuickLaTeX.com \[\delta {A_l} = \lambda \left( {{{\widetilde \Delta }^{ - 1}}} \right)_l^k{\nabla ^j}{\varepsilon _{jkm}}\Sigma = D_{lm}^{ - 1}\left( {\lambda \frac{{\Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }}} \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c20d6f42588c421c51a347368f7e8510_l3.png)
with:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\delta \Sigma = - \lambda {\varepsilon ^{ijk}}{{\partial }_j}{A_k}}\\{\delta \theta = \lambda \frac{{i{\tau _2}}}{2}\theta }\\{\delta {\pi _\theta } = - {\pi _\theta }\lambda \frac{{i{\tau _2}}}{2}}\\{\delta \chi = 0}\\{\delta P = 0}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d14f59cb9fd46c067ac74a8182fb9a89_l3.png)
and so we obtain:
![]()
where:
![Rendered by QuickLaTeX.com \[{\Sigma ^{ * \dagger }} = \Sigma - \sqrt {\gamma _{ij}^{D3}} \left( {{\Delta ^{ - 1}}} \right)\left( {{\nabla _{lm}}\frac{{\Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }}} \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-30286b808524bc74f025b7b767438759_l3.png)
We are now in a position to derive the Dp/M5-brane Hamiltonian. The bosonic D-brane Lagrangian has the general form:
![]()
![]()
where ![]() is the Hodge dual of a p-form potential and
is the Hodge dual of a p-form potential and ![]() is the Hamiltonian density given as such:
is the Hamiltonian density given as such:
![]()
with:
![Rendered by QuickLaTeX.com \displaystyle \left\{ {\begin{array}{*{20}{c}} {{{\mathcal{T}}_{i}}=-{{\partial }_{i}}{{T}_{{Dp}}}} \\ {\tilde{K}=-{{\partial }_{i}}{{{\bar{E}}}^{i}}+{{{(-)}}^{{p+1}}}{{T}_{{Dp}}}S} \\ {S=*{{{\left( {\tilde{R}{{e}^{{\tilde{F}}}}} \right)}}_{p}}} \\ {{{\mathcal{H}}_{i}}={{{\bar{P}}}_{a}}E_{i}^{a}+{{{\bar{E}}}^{j}}{{{\tilde{F}}}_{{ij}}}} \\ {E_{i}^{a}=E_{m}^{a}{{\partial }_{i}}{{X}^{m}}} \\ {\mathcal{H}=\frac{1}{2}\left[ {{{{\bar{P}}}^{2}}+{{{\bar{E}}}^{j}}{{{\bar{E}}}^{j}}{{{\tilde{G}}}_{{ij}}}+{{T}_{{Dp}}}{{e}^{{-2\phi }}}\det \left( {{{{\tilde{G}}}_{{ij}}}+{{{\tilde{F}}}_{{ij}}}} \right)} \right]} \end{array}} \right.](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1cba0b2314f1c1955d6ae741fa673281_l3.png)
Hence we have constant brane-tension, abelian p-form gauge transformations, gauge field transformations satisfying Gauss’s law, and that ![]() and
and ![]() generate worldvolume diffeomorphisms and time translations. Since the RR field strength
generate worldvolume diffeomorphisms and time translations. Since the RR field strength ![]() with WZ coupling acts as a Gaussian-law source, we can derive the following:
with WZ coupling acts as a Gaussian-law source, we can derive the following:
![Rendered by QuickLaTeX.com \displaystyle \left\{ {\begin{array}{*{20}{c}} {{{{\bar{P}}}_{a}}={{E}_{a}}^{m}\left( {{{P}_{m}}+{{E}^{i}}{{Z}^{*}}{{{\left( {{{i}_{m}}B} \right)}}_{i}}+{{T}_{{Dp}}}{{{\tilde{C}}}_{m}}} \right)} \\ {{{{\tilde{C}}}_{m}}=*\left( {{{Z}^{*}}\left( {{{i}_{m}}C} \right)\wedge {{e}^{{\tilde{F}}}}} \right)} \\ {{{{\bar{E}}}^{i}}={{E}^{i}}+T{{{\tilde{C}}}^{i}}} \\ {{{{\tilde{C}}}^{i}}={{{\left[ {*{{{\left( {\tilde{C}{{e}^{{\tilde{F}}}}} \right)}}_{{p-1}}}} \right]}}^{i}}} \end{array}} \right.](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4f2e504f60812fd9cf893f5749cbcee7_l3.png)
and hence the Hamiltonian phase-space constraint is quartic, as required. The Hamiltonian for the M5-brane breaks ![]() into
into ![]() . Working with the worldvolume metric
. Working with the worldvolume metric ![]() and its inverse
and its inverse ![]() , we get the following:
, we get the following:
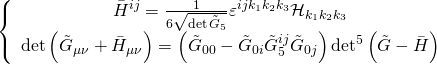
with ![]() the determinant of the worldvolume form
the determinant of the worldvolume form ![]() and:
and:
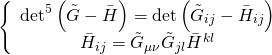
Thus, the phase-space M5-brane bosonic Lagrangian is given by:
![]()
where:
![]()
are given as such:
![]()
![]()
![]()
By the Bianchi identify for ![]() , we have:
, we have:
![]()
and the last three functionals in:
![]()
are given by:
![]()
![]()
![]()
and they correspond, respectively, to generating-functionals for time-translation, worldvolume diffeomorphism and self-duality, with the following relations holding:
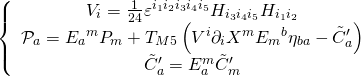
In summary, the M5-![]() algebra closes and the D3-brane self-dual Hamiltonian action is invariant under linear
algebra closes and the D3-brane self-dual Hamiltonian action is invariant under linear ![]() transformation:
transformation:
![]()
and rotations of ![]() by:
by:
![]()
and non-linear transformation of the background ![]() and
and ![]() .
.
