The D-brane superpotential, a section of special holomorphic line bundles of the complex and Kähler product moduli space, and hence the correlation-function generator, is pivotal for at least three central reasons in the construction of Calabi-Yau compactifications: first, for allowing M-theory compactifications on Kovalev twisted connected sum ![]() -manifolds. Second, for giving rise to Yukawa couplings, and consequently, allows us to determine the vacuum of the low energy N=1 effective theory. And third, to allow for topological CY properties such as Jones-Witten and Ooguri–Vafa invariants. In this post, we will analyze the D-brane superpotential for pseudo-Fermat Calabi-Yau manifolds via mirror symmetry and the Gel’fand-Kapranov-Zelevinski hypergeometric system in the context of Saito’s differential equations of deformation theory of singularities and derive an Aganagic-Klemm-Vafa type mirror symmetry based on the Witten equation. First, let us set the stage. Dp-brane solutions preserving half supersymmetry have general form:
-manifolds. Second, for giving rise to Yukawa couplings, and consequently, allows us to determine the vacuum of the low energy N=1 effective theory. And third, to allow for topological CY properties such as Jones-Witten and Ooguri–Vafa invariants. In this post, we will analyze the D-brane superpotential for pseudo-Fermat Calabi-Yau manifolds via mirror symmetry and the Gel’fand-Kapranov-Zelevinski hypergeometric system in the context of Saito’s differential equations of deformation theory of singularities and derive an Aganagic-Klemm-Vafa type mirror symmetry based on the Witten equation. First, let us set the stage. Dp-brane solutions preserving half supersymmetry have general form:
![]()
![]()
![]()
![]()
where the Hamiltonian metaplectic action in the Heisenberg representation on the Dp+1 dimensional worldvolume gives us:
![]()
where:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\Im _i} = - \not \partial {\phi _{si}}{T_{Dp}}d\,\Omega {{({\phi _{si}})}^{2\pi ik}}}\\{\not K = - {{\not \partial }_i}{{\widetilde E}^i} + {{( - 1)}^{p + 1}}{T_{Dp}}{S^{{\rm{Fer}}}}}\\{{{\not H}_i} = \widetilde P{\alpha _i}\widetilde E_i^\alpha {{\not \partial }_i}{\phi _{si}} + \widetilde E{{\not F}_{ij}}}\\{H = \frac{1}{{2\pi ik}}\left[ {{{\widetilde P}^2} + {{\widetilde E}^i}{{\widetilde E}^j}{G_{ij}} + T_{Dp}^2{e^{ - 2{\phi _{si}}}}{\rm{det}}\left( {{G_{ij}} + {{\not F}_{ij}}} \right)} \right]}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bd828556ea51b8c78862eb753658693f_l3.png)
with:
![]()
and:
![]()
where the Ramond-Ramond gauge-coupling sector is given by the action:
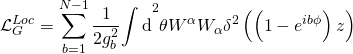
and generally, the action of a ![]() -brane is given by a Dirac-Born-Infeld part coupled to a Chern-Simons WZ part:
-brane is given by a Dirac-Born-Infeld part coupled to a Chern-Simons WZ part:
![]()
with:
![]()
![]()
where ![]() is the worldvolume pullback with
is the worldvolume pullback with ![]() -orientifold action:
-orientifold action:
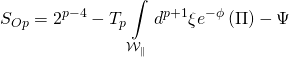
with:
![]()
and
![]()
where the pullback to the ![]() -worldvolume yields the 10-D SYM action:
-worldvolume yields the 10-D SYM action:
![]()
with string coupling:
![]()
and the 10-D SUGRA dimensionally reduced Type-IIB action is:
![]()
with:
![]()
![]()
![]()
and in the string-frame, the type-IIB SUGRA action is given by:
![]()
with:
![]()
![]()
![]()
where the Calabi-Yau superpotential is:
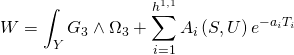
where:
![]()
is the Gukov-Vafa-Witten superpotential stabilization complex term, as well as the axio-dilaton field:
![]()
Given the presence of ![]() -brane instantons,
-brane instantons, ![]() are of Kähler moduli Type-IIB-orbifold class:
are of Kähler moduli Type-IIB-orbifold class:
![]()
with ![]() being the volume of the divisor
being the volume of the divisor ![]() and
and ![]() the 4-form Ramond-Ramond axion field corresponding to:
the 4-form Ramond-Ramond axion field corresponding to:
![]()
and:
![]()
where ![]() is the Kähler form:
is the Kähler form:
![]()
and:
![]()
an integral-form basis and ![]() the associated intersection coefficients. Hence, the Kähler potential is given by:
the associated intersection coefficients. Hence, the Kähler potential is given by:
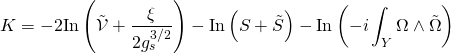
with ![]() the Calabi-Yau volume, and in the Einstein frame, is given by:
the Calabi-Yau volume, and in the Einstein frame, is given by:
![]()
The ![]() -term is given by:
-term is given by:
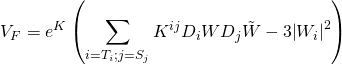
with the Large Volume Scenario ![]() -term is given by:
-term is given by:
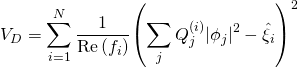
with:
![]()
and the Fayet-Illopoulos terms being:
![]()
where ![]() are the
are the ![]() -brane charge-vectors. Then we saw that the Chern-Simons orientifold action gets a Calabi-Yau curvature correction in the form of:
-brane charge-vectors. Then we saw that the Chern-Simons orientifold action gets a Calabi-Yau curvature correction in the form of:
![Rendered by QuickLaTeX.com \displaystyle {{S}_{{{{O}_{p}},CS}}}=-{{2}^{{p-4}}}-{{T}_{p}}\int\limits_{{{{\mathcal{W}}^{\prime }}}}{{P\left[ C \right]}}\wedge \Theta](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-371c7b529216d796ebd4b8241427e1d1_l3.png)
with
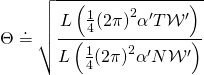
due to the Gauss–Codazzi equations:
![]()
and the Ramond-Ramond term being:
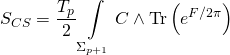
which yields the Type-IIB Calabi-Yau three-fold superpotential:
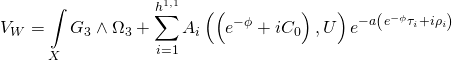
and where the topologically mixed Yang-Mills action is given by:
![]()
with the corresponding Chern-Simons action:
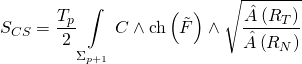
Generically, type-II compactifications on Calabi–Yau manifolds give rise to N=1 low energy effective theories given suitable background fluxes and space-filling D-branes wrapping internal special Lagrangian sub-manifolds and holomorphic divisors determined by period integrals satisfying systems of Picard-Fuchs differential equations where the period integrals of the holomorphic three-form whose cycles have boundaries wrapped by D-branes determine the effective superpotential. The associated superpotential of D-branes wrapping internal cycles of Calabi–Yau manifold ![]() is given as such:
is given as such:
![]()
In the Type-II case, it is a linear sum of the period integrals:
![]()
with:
![]()
The Ramond-Ramond and Neveu-Schwarz background fluxes ![]() ,
, ![]() yield the flux-superpotential:
yield the flux-superpotential:
![]()
Thus, putting the two superpotentials together gives us:
![]()
where ![]() is the D-brane topological charge and
is the D-brane topological charge and ![]() is the period-integral over the CY 3-form:
is the period-integral over the CY 3-form:
![]()
and the domain-wall tension is given by:
![]()
Now, in the A-model, the D-brane superpotential is defined in terms of closed/open holomorphic correlation-functional coordinates determined by OPE coefficients corresponding to the worldsheet chiral ring:
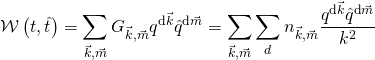
where we have:
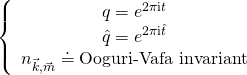
and the following relations follow for the D-brane superpotential and the Ooguri–Vafa invariants:
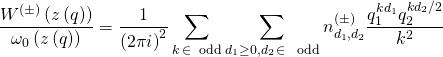
and:
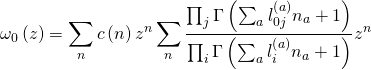
where the mirror-symmetry map is given by:
![]()
We now define a mirror pair of hypersurfaces ![]() in toric ambient spaces
in toric ambient spaces ![]() with corresponding fans
with corresponding fans ![]() , where the hypersurface defining polynomial is given as such:
, where the hypersurface defining polynomial is given as such:
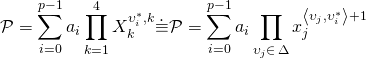
It is clear that a GKZ hypergeometric differential system:
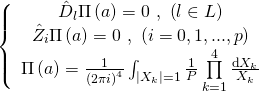
with:
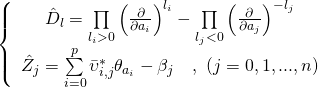
annihilates the integral periods, and the torus invariant Kähler coordinates of the system are given as such:
![]()
generating the Mori cone. Now, since we have:
![]()
we get:
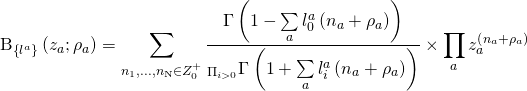
Now let us consider Saito’s system of DE of deformations of a singularity. Take a sheaf ![]() of germs of relative holomorphic
of germs of relative holomorphic ![]() forms for the natural projection
forms for the natural projection ![]() . One consider now sheaves on S with the following properties:
. One consider now sheaves on S with the following properties:
![]()
![]()
We now take an image of a primitive form ![]() in
in ![]() :
:
![]()
Let us connect the Gel’fand-Leray form to the Saito period integral and the GKZ system. The defining singularity polynomial equation for singularity ![]() reflecting a monodromy action, is:
reflecting a monodromy action, is:
![]()
for a deformation:
![]()
where the parameters ![]() act as a coordinate system of:
act as a coordinate system of:
![]()
There is then a natural map:
![]()
Now we focus on the sheaf ![]() of germs of holomorphic p-forms for the projection
of germs of holomorphic p-forms for the projection ![]() of form:
of form:
![]()
![]()
Hence, we can re-write the image of the primitive form as such:
![]()
Now the Saito’s system is characterized as a set of differential equations satisfied by the PF:
![]()
![]()
We can now prove the following:
With ![]() the roots of
the roots of ![]() satisfying
satisfying ![]() , the space of the solutions to Saito’s system is generated by:
, the space of the solutions to Saito’s system is generated by:
![]()
with a singularity at the discriminant locus:
![]()
and where the monodromy group about the discriminant is isomorphic to the order-![]() symmetric group
symmetric group ![]() among the roots
among the roots ![]() s.
s.
Note that now we have a defining equation:
![]()
where we take the canonical torus action ![]() on
on ![]() :
:
![]()
The Saito system now naturally relates to a Gel’fand-Kapranov-Zelevinski system with canonical period integral forms:
![]()
integration is over homology 2-cycle curves on:
![]()
and:
![]()
and up to homotopic rescaling, the period integral satisfies a Gel’fand-Kapranov-Zelevinski system. Two central properties follow. The period integral satisfies:
![]()
with respect to the Saito lattice-operator, with:
![]()
and the system is rank-![]() irreducible and the
irreducible and the ![]() -independent solutions are given by:
-independent solutions are given by:
![]()
So the root ![]() of
of ![]() satisfies:
satisfies:
![]()
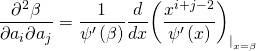
Hence, the independent solutions of the Gel’fand-Kapranov-Zelevinski system:
![]()
are given by:
![]()
whose monodromy transformations properties are given by:
![]()
Hence,
![]()
get annihilated by the operators ![]() . Moreover, we have the following relationship holding:
. Moreover, we have the following relationship holding:
![]()
given that the following holds:
![]()
By recursion, we can derive:
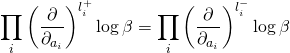
![]()
Now since by definition we have:
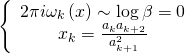
the ![]() ‘s are solutions to the Gel’fand-Kapranov-Zelevinski hypergeometric system, with:
‘s are solutions to the Gel’fand-Kapranov-Zelevinski hypergeometric system, with:
![]()
Now we interpret the Chern-Simons part of the D-brane action as naturally inducing the charge vectors ![]() defining the Calabi-Yau condition, and consider the following operators:
defining the Calabi-Yau condition, and consider the following operators:
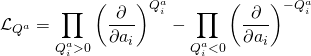
![]()
characterizing the Gel’fand-Kapranov-Zelevinski hypergeometric ![]() -system:
-system:
![]()
Now, for the Calabi-Yau manifolds that arise as hypersurfaces in toric varieties, the above Gel’fand-Kapranov-Zelevinski equations are analytically related by a Witten deformation to the above Picard-Fuchs equations. Under the change of variables:
![]()
and:
![]()
the corresponding Gel’fand-Kapranov-Zelevinski system obtained allows us to derive the open-string instanton effects exactly as in the bulk Gel’fand-Kapranov-Zelevinski for the closed-string case. Take the following operators:
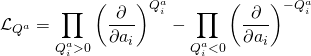
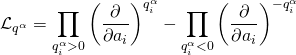
![]()
which is the Gel’fand-Kapranov-Zelevinski HGS that naturally corresponds to the boundary toric variety, and under the c.o.v.:
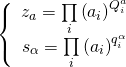
yields an open/closed bulk/boundary duality supporting Witten mirror flops and flips in the dual character-torus lattice of the Calabi-Yau:
![]()
For the Aganagic-Klemm-Vafa system, the solution corresponding to the D-brane superpotential are given as so:
![]()
where ![]() is the Witten superpotential satisfying the Witten equation:
is the Witten superpotential satisfying the Witten equation:
![]()
whose Picard-Lefschetz virtual fundamental cycles:
![Rendered by QuickLaTeX.com \displaystyle \left\{ {\begin{array}{*{20}{c}} {{{{\left[ {{\bar{\mathcal{W}}}'_{{g,k}}^{{rig}}\left( {{{k}_{{{{j}_{1}}}}},...,{{k}_{{{{j}_{k}}}}}} \right)} \right]}}^{{vir}}}} \\ {\deg \quad 2\left( {\left( {{{{\hat{c}}}_{W}}-3} \right)\left( {g-1} \right)+k-\sum\limits_{i}{{{{\iota }_{{{{\gamma }_{i}}}}}}}} \right)-\sum\limits_{i}{{{{N}_{{{{\gamma }_{i}}}}}}}} \end{array}} \right.](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-01b8e2d55507e8a566bad663af551ef6_l3.png)
naturally induce Witten mirror moduli flops and flips bulk/boundary duality associated to the Aganagic-Klemm-Vafa disk instantons defined by the Gel’fand-Kapranov-Zelevinski system.
It can be shown that all flips and flops in the dual character-torus lattice of the Calabi-Yau moduli space corresponding to an M-theory compactification arise naturally in this way.