Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

The Lindblad Collapse Equation and Quantum Decoherence

By Posted on In Mathematical Physics, Mathematics, Philosophy, Philosophy Of Physics, Physics ,
Quantum Decoherence

Continuing from where I left off revealing paradoxical aspects of wave-function collapse involving time-reversal symmetry and the quantum entanglement of the total system consisting of ‘S’, ‘m’ and the quantum-time measuring clock ‘c’ subject to Heisenberg’s UP, consider the collapse equation:

    \[\begin{array}{*{20}{l}}{d{\psi _t}^{S,m,c} = \left[ { - iHdt + \sum\limits_{k = 1}^n {\left( {{L_k} - {\ell _{k,t}}} \right)} } \right.}\\{d{W_{k,t}} - \frac{1}{2}\sum\limits_{k = 1}^n {\left. {\left( {L_k^\dagger {L_k} - 2{\ell _{k,t}}{L_k} + {{\left| {{\ell _{k,t}}} \right|}^2}} \right)} \right]} }\\{{\psi _t}^{S,m,c}}\end{array}\]

with {L_k} the Hilbert-space Lindblad collapse operators, {\ell _{k,t}} given by:

    \[{\ell _{k,t}} \equiv \frac{1}{2}\left\langle {{\psi _t},\left( {L_k^\dagger + {L_k}} \right){\psi _t}^{S,m,c}} \right\rangle \]

and the first term on the right-hand side represents the unitary quantum evolution, the rest the collapse of the wave-function. Dynamically, to ensure the positivity of the reduced density matrix:

    \[\forall t\left\langle {\left. \psi \right|{{\hat \rho }_S}(t)\left| \psi \right.} \right\rangle \ge 0\]

the Lindblad collapse equation:

    \[\begin{array}{*{20}{l}}{d\left| {{\psi _t}^{S,m,c}} \right\rangle = \left[ { - \frac{i}{\hbar }} \right.Hdt + \sqrt \lambda \int {{d^3}} x\left( {N(\bar x) - {{\left\langle {N(\bar x)} \right\rangle }_t}} \right)}\\{d{W_t}(\bar x) - \frac{\lambda }{2}\int {{d^3}} x\left. {{{\left( {N(\bar x) - {{\left\langle {N(\bar x)} \right\rangle }_t}} \right)}^2}dt} \right]\left| {{\psi _t}^{S,m,c}} \right\rangle }\end{array}\]

would entail that the Lindblad quantum-jump equation:

    \[\begin{array}{l}{\rm{d}}\hat \rho _S^C = - i\left[ {{{\hat H}_S},\hat \rho _S^C} \right]{\rm{d}}t - \\\frac{1}{2}\sum\limits_\mu {{\kappa _\mu }} \left[ {{{\hat L}_\mu },\left[ {{{\hat L}_\mu },\hat \rho _S^C} \right]} \right]{\rm{d}}t + \\\sum\limits_\mu {\sqrt {{\kappa _\mu }} } W\left[ {{{\hat L}_\mu }} \right]\hat \rho _S^C{\rm{d}}{W_\mu }\end{array}\]

is solvable iff  {L_k} commutes with the position-operator, with:

    \[\begin{array}{l}W\left[ {\hat L} \right]\hat \rho \equiv \hat L\hat \rho + \hat \rho {{\hat L}^\dagger } - \\\hat \rho {\rm{Tr}}\left\{ {\hat L\hat \rho + \hat \rho {{\hat L}^\dagger }} \right\}\end{array}\]

where \rho is the the Markovian reduced density operator, and {\rm{d}}{W_\mu } the Weiner-quantum-increments.

However:

    \[\tilde U: = - \frac{\lambda }{2}\int {{d^3}} x{\left( {N(\bar x) - {{\left\langle {N(\bar x)} \right\rangle }_t}} \right)^2}dt(...)\]

commutes with the energy operator. By the Heisenberg energy-time uncertainty principle, the collapse equation cannot be integrated to get the collapse-localization double-integral in 4-D:

    \[{\int {\int {\left| {\Psi _{{t_4}}^I\left( {x,X} \right) + \Psi _{{t_4}}^{II}\left( {x,X} \right)} \right|} } ^2}dxdX = 1\]

Now applying the wave-particle duality to:

    \[\int { - \frac{\lambda }{2}} {d^3}xd{W_t}(\bar x) + \int {\frac{i}{\hbar }Hdt + \sqrt \lambda \int {{d^3}} xd{W_t}(\bar x)} \]

implies therefore, by the time-local non-Markovian master equation:

    \[\frac{{\rm{d}}}{{{\rm{d}}t}}{\hat \rho _S}(t) = \hat K(t){\hat \rho _S}(t)\]

that the Lindblad quantum-jump equation is ill-defined over any quantum state describing the total system: in particular, a quantum-time measuring clock (QTMC). This much is guaranteed by the Heisenberg uncertainty principle relating time and energy. Thus, since such a QTMC is essential for Schrödinger’s equation, the paradox is now clear.

Let us look at how quantum Markovian jumps can offer a decoherence way out. Let a system S be described by the master equation for the reduced density operator in the Markovian approximation:

    \[\begin{array}{c}\dot \rho = i\left[ {\hat H,\rho } \right] + \sum\limits_m {{{\hat L}_m}} \hat L_m^\dagger - \frac{1}{2}\hat L_m^\dagger {{\hat L}_m}\rho \\ - \frac{1}{2}\rho \hat L_m^\dagger {{\hat L}_m}\end{array}\]

which has a Heisenberg-cut unraveling into a quantum jump process for pure states, with the usual Hamiltonian and the Lindblad operators which describe the effects of the environment are the set \left\{ {{{\hat L}_m}} \right\}. Here, I am describing quantum systems via an exhaustive set of possible histories that satisfy a decoherence or consistency-histories criterion obeying the classical probability sum rules. Moreover, such quantum jumps are interpreted as yielding the values of continuous measurements and the histories correspond to records of a classical measuring device that must decohere. Hence, there is a set of decoherent histories that correspond to the quantum trajectories of a continuously measured system. See Ian Percival as well as Lajos Diósi for such remarkable correspondences.

Now take a quantum system with a Hamiltonian {\hat H_0} with complete single channel of decay tracked by an external photon detector described by a model of a single 2-level system with states \left| 0 \right\rangle and \left| 1 \right\rangle strongly coupled to an environment representing the remaining degrees of freedom. The two crucial properties are clearly, 1) dissipation: Excitations of the states absorbed by the measuring device with a rate {\Gamma _1}, with the time-resolution of the detector given by 1/{\Gamma _1}, and 2) decoherence: As output mode states become correlated with the internal degrees of freedom of the measuring device, the phase coherence between the ground and excited states of the output mode is completely and tracelessly lost, 

and the loss of coherence is far quicker than the actual rate of energy loss, with decoherence rate {\Gamma _2} \gg {\Gamma _1}

So, the linearized system coupled to the output mode via the Hamiltonian:

    \[{\hat H_I} = \kappa \left( {{{\hat a}^\dagger } \otimes \hat b + \hat a \otimes {{\hat b}^\dagger }} \right)\]

with the following total Hamiltonian:

    \[\hat H = {\hat H_0} \otimes \hat 1 + \kappa \left( {{{\hat a}^\dagger } \otimes \hat b + \hat a \otimes {{\hat b}^\dagger }} \right)\]

with \left( {\hat a,\hat b} \right);\left( {{{\hat a}^\dagger },{{\hat b}^\dagger }} \right) the lowering/raising operators for the system and output mode respectively entails that the total system satisfies the master equation:

    \[\begin{array}{c}\dot \rho = - i\left[ {\hat H,\rho } \right] + {\Gamma _1}\hat b\rho {{\hat b}^\dagger } - \frac{{{\Gamma _1}}}{2}{{\hat b}^\dagger }\hat b\rho \\ - \frac{{{\Gamma _1}}}{2}\rho {{\hat b}^\dagger }\hat b + {\Gamma _2}{\sigma _z}\rho {\sigma _z} - {\Gamma _2}\rho \\ \equiv L_s^L\rho \end{array}\]

where the Pauli operator {\sigma _z} acts on the output mode and L_s^L is the Liouville superoperator. Given that it is a linear equation, it has a solution given as:

    \[\rho ({t_2}) = \exp \left\{ {L_s^L\left( {{t_2} - {t_1}} \right)} \right\}\rho ({t_1})\]

Start with a pure state:

    \[\left| \Psi \right\rangle = \left| \psi \right\rangle \otimes \left| 0 \right\rangle \]

and expand \rho as:

    \[\begin{array}{l}\rho (t) = {\rho _{00}}(t) \otimes \left| 0 \right\rangle \left\langle 0 \right| + {\rho _{01}}(t)\\ \otimes \left| 0 \right\rangle \left\langle 1 \right| + {\rho _{10}}(t) \otimes \left| 1 \right\rangle \left\langle 0 \right| + {\rho _{11}}(t)\\ \otimes \left| 1 \right\rangle \left\langle 1 \right|\end{array}\]

So the master equation reduces component-wise to:

    \[\begin{array}{c}{{\dot \rho }_{00}} = - \left[ {\hat H,{\rho _{00}}} \right] - i\kappa {{\hat a}^\dagger }{\rho _{10}} + i\kappa {\rho _{01}}\hat a\\ + {\Gamma _1}{\rho _{11}}\end{array}\]

    \[\begin{array}{l}{{\dot \rho }_{01}} = - \left[ {\hat H,{\rho _{01}}} \right] - i\kappa {{\hat a}^\dagger }{\rho _{11}} + i\kappa {\rho _{00}}{{\hat a}^\dagger }\\ - G{\rho _{01}} = \dot \rho _{10}^\dagger \end{array}\]

and

    \[\begin{array}{c}{{\dot \rho }_{11}} = - \left[ {\hat H,{\rho _{11}}} \right] - i\kappa \hat a{\rho _{10}} + i\kappa {\rho _{10}}{{\hat a}^\dagger }\\ - {\Gamma _1}{\rho _{11}}\end{array}\]

with:

    \[G = {\Gamma _1}/2 + 2{\Gamma _2} \gg {\Gamma _1} \gg \kappa \]

Now, given that the {\rho _{01}},{\rho _{10}},{\rho _{11}} components are heavily damped, one can adiabatically eliminate all except {\rho _{00}}:

    \[\begin{array}{l}{{\dot \rho }_{00}} = - i\left[ {{{\hat H}_0},{\rho _{00}}} \right] + \frac{{2{\kappa ^2}}}{G}\hat a{\rho _{00}}{{\hat a}^\dagger }\\ - \frac{{{\kappa ^2}}}{G}{{\hat a}^\dagger }\hat a{\rho _{00}} - \frac{{{\kappa ^2}}}{G}{\rho _{00}}{{\hat a}^\dagger }\hat a\end{array}\]

Such a master equation can be fleshed out as a sum over quantum jump trajectories. So, let us define a non-Hermitian effective Hamiltonian:

    \[{\hat H_{eff}} = {\hat H_0} - i\left( {{\kappa ^2}/G} \right){\hat a^\dagger }\hat a\]

Hence, \psi _t^{S,m,c} evolves according to the Schrödinger equation:

    \[\frac{{d\left| {\psi _t^{S,m,c}} \right\rangle }}{{dt}} = - \frac{i}{\hbar }{\hat H_{eff}}\left| {\psi _t^{S,m,c}} \right\rangle \]

with interruptions at random times by sudden quantum jumps:

    \[\left| {\psi _t^{S,m,c}} \right\rangle \to \hat a\left| {\psi _t^{S,m,c}} \right\rangle \]

that correspond to informational detection of photons.

and this is key: the evolution does not preserve the norm of the state. The physical state is 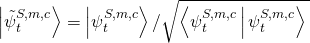\left| {\tilde \psi _t^{S,m,c}} \right\rangle = \left| {\psi _t^{S,m,c}} \right\rangle /\sqrt {\left\langle {\psi _t^{S,m,c}\left| {\left. {\psi _t^{S,m,c}} \right\rangle } \right.} \right.}, the renormalized state

It follows then that the probability that any given initial state \left| {\psi _t^{S,m,c}} \right\rangle evolves for a time T that undergoes N jumps during intervals \delta t centered at times {t_1},...,{t_N} is given by:

    \[\begin{array}{l}{\left( {2\delta t{\kappa ^2}/G} \right)^N}{\rm{Tr}}\left\{ {{e^{ - i{{\tilde H}_{eff}}\left( {T - {t_N}} \right)}}} \right. \cdot \\\hat a{e^{ - i{{\hat H}_{eff}}}}\left( {{t_N} - {t_{N - 1}}} \right)\hat a...\,\hat a{e^{ - i{{\hat H}_{eff}}t}}\\ \times \left| {\psi _t^{S,m,c}} \right\rangle \left\langle {\psi _t^{S,m,c}} \right|{e^{i{{\tilde H}^\dagger }_{eff}{t_1}}}{{\hat a}^\dagger }...\,\left. {{{\hat a}^\dagger }{e^{i{{\tilde H}^\dagger }_{eff}\left( {T - {t_N}} \right)}}} \right\}\end{array}\]

So, the master equation:

    \[\begin{array}{l}{{\dot \rho }_{00}} = - i\left[ {{{\hat H}_0},{\rho _{00}}} \right] + \frac{{2{\kappa ^2}}}{G}\hat a{\rho _{00}}{{\hat a}^\dagger }\\ - \frac{{{\kappa ^2}}}{G}{{\hat a}^\dagger }\hat a{\rho _{00}} - \frac{{{\kappa ^2}}}{G}{\rho _{00}}{{\hat a}^\dagger }\hat a\end{array}\]

is valid iff the Markovian approximation is faithful and valid only on time-scales longer than 1/{\Gamma _1}, hence the jump occurs during an interval \delta t \sim 1/{\Gamma _1} centered on {t_i}.

Now, by taking the average of \left| {\tilde \psi _t^{S,m,c}} \right\rangle \left\langle {\tilde \psi _t^{S,m,c}} \right| over all possible trajectories with the probability measure:

    \[\begin{array}{l}{\left( {2\delta t{\kappa ^2}/G} \right)^N}{\rm{Tr}}\left\{ {{e^{ - i{{\tilde H}_{eff}}\left( {T - {t_N}} \right)}}} \right. \cdot \\\hat a{e^{ - i{{\hat H}_{eff}}}}\left( {{t_N} - {t_{N - 1}}} \right)\hat a...\,\hat a{e^{ - i{{\hat H}_{eff}}t}}\\ \times \left| {\psi _t^{S,m,c}} \right\rangle \left\langle {\psi _t^{S,m,c}} \right|{e^{i{{\tilde H}^\dagger }_{eff}{t_1}}}{{\hat a}^\dagger }...\,\left. {{{\hat a}^\dagger }{e^{i{{\tilde H}^\dagger }_{eff}\left( {T - {t_N}} \right)}}} \right\}\end{array}\]

the unraveling reproduces the master equation:

    \[\begin{array}{l}{{\dot \rho }_{00}} = - i\left[ {{{\hat H}_0},{\rho _{00}}} \right] + \frac{{2{\kappa ^2}}}{G}\hat a{\rho _{00}}{{\hat a}^\dagger }\\ - \frac{{{\kappa ^2}}}{G}{{\hat a}^\dagger }\hat a{\rho _{00}} - \frac{{{\kappa ^2}}}{G}{\rho _{00}}{{\hat a}^\dagger }\hat a\end{array}\]

let us consider now the decoherent histories picture

A set of decoherent histories for a system is given by choosing a complete set of projections:

    \[\left\{ {\hat P_{{\alpha _j}}^j({t_j})} \right\}\]

at a sequence of times {t_1},...\,{t_N} representing exclusively different alternatives histories:

    \[\left\{ {\begin{array}{*{20}{c}}{\sum\limits_{{\alpha _j}} {\hat P_{{\alpha _j}}^j\left( {{t_j}} \right) = \hat 1} }\\{\hat P_{{\alpha _j}}^j\left( {{t_j}} \right)\hat P_{{{\alpha '}_j}}^j\left( {{t_j}} \right) = {\delta _{{\alpha _j}{{\alpha '}_j}}}\hat P_{{\alpha _j}}^j\left( {{t_j}} \right)}\end{array}} \right.\]

A history h is given by picking one \hat P at each point in time. Then the decoherence functional for a given pair of histories h and h' is:

    \[\begin{array}{l}{D^{dec}}\left[ {h,h'} \right] = {\rm{Tr}}\left\{ {\hat P_{{\alpha _N}}^N\left( {{t_N}} \right)...\hat P_{{\alpha _1}}^1} \right.\left( {{t_1}} \right)\\\rho \left( {{t_0}} \right)\hat P_{{{\alpha '}_1}}^1\left( {{t_1}} \right)...\left. {\hat P_{{{\alpha '}_N}}^N} \right\}\end{array}\]

and satisfies the decoherence criterion iff the off-diagonal terms vanish, that is:

    \[{D^{dec}}\left[ {h,h'} \right] = 0\;;\quad h \ne h'\]

Now take any initial pure state:

    \[\left| \Psi \right\rangle = \left| {\psi _0^{S,m,c}} \right\rangle \otimes \left| 0 \right\rangle \]

and take histories composed only of the Schrödinger-projections:

    \[\left\{ {\begin{array}{*{20}{c}}{{{\hat P}_{S,0}} = \hat 1 \otimes \left| 0 \right\rangle \left\langle 0 \right|}\\{{{\hat P}_{S,1}} = \hat 1 \otimes \left| 1 \right\rangle \left\langle 1 \right|}\end{array}} \right.\]

characterizing the absence or presence of an m-photon in the output mode. Schrödinger-projections are spaced \delta t-apart, and a history consists of N projections representing a total time T = N\delta t. Using the quantum regression theorem, the above decoherence functional reduces to:

    \[\begin{array}{l}{D^{dec}}\left[ {h,h'} \right] = {\rm{Tr}}\left\{ {{{\hat P}_{{\alpha _N}}}} \right.{e^{L_s^L\delta t}}\left( {{{\hat P}_{{\alpha _{N - 1}}}}{e^{L_s^L\delta t}}} \right.\\\left( {...} \right.{e^{L_s^L\delta t}}\left( {{{\hat P}_{{\alpha _1}}}} \right.\left| \Psi \right\rangle \left\langle \Psi \right.\left| {\left. {{{\hat P}_{{\alpha _1}}}} \right)} \right.\left. {...} \right)\left. {{{\hat P}_{{\alpha _N}}}} \right\}\end{array}\]

and the Liouville time evolution superoperators:

    \[\rho ({t_2}) = \exp \left\{ {L_s^L\left( {{t_2} - {t_1}} \right)} \right\}\rho ({t_1})\]

transform pure states into mixed states.

So, from:

    \[\begin{array}{c}{{\dot \rho }_{00}} = - \left[ {\hat H,{\rho _{00}}} \right] - i\kappa {{\hat a}^\dagger }{\rho _{10}} + i\kappa {\rho _{01}}\hat a\\ + {\Gamma _1}{\rho _{11}}\end{array}\]

    \[\begin{array}{l}{{\dot \rho }_{01}} = - \left[ {\hat H,{\rho _{01}}} \right] - i\kappa {{\hat a}^\dagger }{\rho _{11}} + i\kappa {\rho _{00}}{{\hat a}^\dagger }\\ - G{\rho _{01}} = \dot \rho _{10}^\dagger \end{array}\]

and

    \[\begin{array}{c}{{\dot \rho }_{11}} = - \left[ {\hat H,{\rho _{11}}} \right] - i\kappa \hat a{\rho _{10}} + i\kappa {\rho _{10}}{{\hat a}^\dagger }\\ - {\Gamma _1}{\rho _{11}}\end{array}\]

one can uniquely determine the character of the different histories, and the central regime is in the range:

    \[\frac{1}{G} \ll \delta t \gg \frac{1}{{{\Gamma _1}}}\]

Note, the {\Gamma _2} terms on this time-scale are sufficient to guarantee decoherence and what is crucial is that the {\Gamma _1} terms resolve into individual pure state trajectories: and that is because

the probability of a photon being emitted in any single time-step is small yet any emission implies there is a non-zero probability of absorption on a time scale 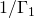1/{\Gamma _1}

The decoherence-effect effectively gives rise to the terms:

    \[\left\{ {\begin{array}{*{20}{c}}{\left( {{\kappa ^2}/G} \right){{\hat a}^\dagger }\hat a{\rho _{00}}}\\{\left( {{\kappa ^2}/G} \right){\rho _{00}}{{\hat a}^\dagger }\hat a}\end{array}} \right.\]

in equation:

    \[\begin{array}{l}{{\dot \rho }_{00}} = - i\left[ {{{\hat H}_0},{\rho _{00}}} \right] + \frac{{2{\kappa ^2}}}{G}\hat a{\rho _{00}}{{\hat a}^\dagger }\\ - \frac{{{\kappa ^2}}}{G}{{\hat a}^\dagger }\hat a{\rho _{00}} - \frac{{{\kappa ^2}}}{G}{\rho _{00}}{{\hat a}^\dagger }\hat a\end{array}\]

and are factored in the effective Hamiltonian:

    \[{\hat H_{eff}} = {\hat H_0} - i\left( {{\kappa ^2}/G} \right){\hat a^\dagger }\hat a\]

and such terms are fundamental on a time-scale \delta t \ll 1/{\Gamma _1}, unlike \left( {2{\kappa ^2}/G} \right)\hat a{\rho _{00}}{\hat a^\dagger }, which becomes fundamental on a time scale 1/{\Gamma _1}

It is the term:

    \[\left( {2{\kappa ^2}/G} \right)\hat a{\rho _{00}}{\hat a^\dagger }\]

that causes pure states to evolve into mixed states in:

    \[\begin{array}{l}{{\dot \rho }_{00}} = - i\left[ {{{\hat H}_0},{\rho _{00}}} \right] + \frac{{2{\kappa ^2}}}{G}\hat a{\rho _{00}}{{\hat a}^\dagger }\\ - \frac{{{\kappa ^2}}}{G}{{\hat a}^\dagger }\hat a{\rho _{00}} - \frac{{{\kappa ^2}}}{G}{\rho _{00}}{{\hat a}^\dagger }\hat a\end{array}\]

One can maintain the purity of the system-state over a full trajectory by picking a time: \delta t \ll 1/G.

Hence, with:

    \[\rho = {\rho _{00}} \otimes \left| 0 \right\rangle \left\langle 0 \right|\]

and after evolving for a time \delta t, the state becomes:

    \[\begin{array}{*{20}{l}}{{{\left( {{e^{L_s^L\delta t}}\rho } \right)}_{00}} = {\rho _{00}} - i\left[ {{{\hat H}_0},{\rho _{00}}} \right]\delta t}\\{ - \frac{{{\kappa ^2}}}{G}{{\hat a}^\dagger }\hat a{\rho _{00}}\delta t - \frac{{{\kappa ^2}}}{G}{\rho _{00}}{{\hat a}^\dagger }\hat a\delta t + {\rm{h}}.{\rm{o}}.{\rm{t}}}\\{ \approx {e^{ - i\left( {{{\hat H}_0} - i\left( {{\kappa ^2}/G} \right){{\hat a}^\dagger }\hat a} \right)\delta t}}{\rho _{00}}{e^{i\left( {{{\hat H}_0} + i\left( {{\kappa ^2}/G} \right){{\hat a}^\dagger }\hat a} \right)\delta t}}}\end{array}\]

    \[\begin{array}{l}{\left( {{e^{L_s^L\delta t}}\rho } \right)_{01}} = \frac{{i\kappa }}{G}{\rho _{00}}{{\hat a}^\dagger } + {\rm{h}}{\rm{.o}}{\rm{.t}}{\rm{.}} = \\\left( {{e^{L_s^L\delta t}}\rho } \right)_{10}^\dagger \end{array}\]

and

    \[{\left( {{e^{L_s^L\delta t}}\rho } \right)_{11}} = \frac{{2{\kappa ^2}}}{G}\hat a{\rho _{00}}{\hat a^\dagger }\delta t + {\rm{h}}{\rm{.o}}{\rm{.t}}.\]

Thus, the effective Hamiltonian again has two crucial properties. One is the possibility that the excited-mode photon will be absorbed by the measuring device. The second, negligible though, is the possibility that the excited-mode photon will be coherently re-absorbed by the measuring system.

Now, by combining the above three expressions with the projections:

    \[\left\{ {\begin{array}{*{20}{c}}{{{\hat P}_0}}\\{{{\hat P}_1}}\end{array}} \right.\]

we can derive the probabilities for all possible histories. Take the history given by an unbroken string of N {\hat P_0} projections, corresponding to no excited-mode photon being emitted during a time N\,\delta t.

The probability of such a history is the diagonal element of:

    \[\begin{array}{l}{D^{dec}}\left[ {h,h'} \right] = {\rm{Tr}}\left\{ {{{\hat P}_{{\alpha _N}}}} \right.{e^{L_s^L\delta t}}\left( {{{\hat P}_{{\alpha _{N - 1}}}}{e^{L_s^L\delta t}}} \right.\\\left( {...} \right.{e^{L_s^L\delta t}}\left( {{{\hat P}_{{\alpha _1}}}} \right.\left| \Psi \right\rangle \left\langle \Psi \right.\left| {\left. {{{\hat P}_{{\alpha _1}}}} \right)} \right.\left. {...} \right)\left. {{{\hat P}_{{\alpha _N}}}} \right\}\end{array}\]

Now, expanding the time evolution superoperator using:

    \[\begin{array}{*{20}{l}}{{{\left( {{e^{L_s^L\delta t}}\rho } \right)}_{00}} = {\rho _{00}} - i\left[ {{{\hat H}_0},{\rho _{00}}} \right]\delta t}\\{ - \frac{{{\kappa ^2}}}{G}{{\hat a}^\dagger }\hat a{\rho _{00}}\delta t - \frac{{{\kappa ^2}}}{G}{\rho _{00}}{{\hat a}^\dagger }\hat a\delta t + {\rm{h}}.{\rm{o}}.{\rm{t}}}\\{ \approx {e^{ - i\left( {{{\hat H}_0} - i\left( {{\kappa ^2}/G} \right){{\hat a}^\dagger }\hat a} \right)\delta t}}{\rho _{00}}{e^{i\left( {{{\hat H}_0} + i\left( {{\kappa ^2}/G} \right){{\hat a}^\dagger }\hat a} \right)\delta t}}}\end{array}\]

    \[\begin{array}{l}{\left( {{e^{L_s^L\delta t}}\rho } \right)_{01}} = \frac{{i\kappa }}{G}{\rho _{00}}{{\hat a}^\dagger } + {\rm{h}}{\rm{.o}}{\rm{.t}}{\rm{.}} = \\\left( {{e^{L_s^L\delta t}}\rho } \right)_{10}^\dagger \end{array}\]

and

    \[{\left( {{e^{L_s^L\delta t}}\rho } \right)_{11}} = \frac{{2{\kappa ^2}}}{G}\hat a{\rho _{00}}{\hat a^\dagger }\delta t + {\rm{h}}{\rm{.o}}{\rm{.t}}.\]

one can see now that after \delta t we get:

    \[\begin{array}{l}{{\hat P}_0}{e^{L_s^L}}\left( {\left| \psi \right\rangle \left\langle \psi \right| \otimes \left| 0 \right\rangle \left\langle 0 \right|} \right){{\hat P}_0} \approx \\\left( {{e^{ - i\left( {{{\hat H}_0} - i\left( {{\kappa ^2}/G} \right){{\hat a}^\dagger }\hat a} \right)\delta t}}\left| \psi \right\rangle \left\langle \psi \right|{e^{i\left( {{{\hat H}_0} + i\left( {{\kappa ^2}/G} \right){{\hat a}^\dagger }\hat a} \right)\delta t}}} \right)\left| 0 \right\rangle \left\langle 0 \right|\end{array}\]

Taking the trace after N repetitions, one gets:

    \[p(h) \approx {\rm{Tr}}\left\{ {{e^{ - i{{\hat H}_{eff}}N\delta t}}\left| \psi \right\rangle \left\langle \psi \right|{e^{i{{\hat H}^\dagger }_{eff}N\delta t}}} \right\}\]

which is the probability of the quantum jump trajectory when no jumps are detected

Now, let a photon be emitted at time N\delta t and with projection {\hat P_1} instead. The corresponding probability is then:

    \[\begin{array}{l}p(h) \approx \left( {2\delta t{\kappa ^2}/G} \right)\\{\rm{Tr}}\left\{ {\hat a{e^{ - i{{\hat H}_{eff}}N\delta t}}\left| \psi \right\rangle \left\langle \psi \right|{e^{i{{\hat H}^\dagger }_{eff}N\delta t}}{{\hat a}^\dagger }} \right\}\end{array}\]

again, this is the probability of the corresponding quantum jump trajectory

The question then is: what occurs after the output mode has registered as being in the excited state? Two possibilities exist. One is that the output mode drops back to the un-excited state: measuring state absorption, represented by:

    \[\begin{array}{l}{{\hat P}_0}{e^{L_s^L\delta t}}\left( {\left| {\psi '} \right\rangle \left\langle {\psi '} \right| \otimes \left| 1 \right\rangle \left\langle 1 \right|} \right){{\hat P}_0} \approx \\{\Gamma _1}\delta t\left| {\psi '} \right\rangle \left\langle {\psi '} \right| \otimes \left| 0 \right\rangle \left\langle 0 \right|\end{array}\]

Or a constant exited state:

    \[\begin{array}{l}{{\hat P}_1}{e^{L_s^L\delta t}}\left( {\left| {\psi '} \right\rangle \left\langle {\psi '} \right| \otimes \left| 1 \right\rangle \left\langle 1 \right|} \right){{\hat P}_1} \approx \\\left( {1 - {\Gamma _1}\delta t} \right){e^{ - i{{\hat H}_{eff}}\delta t}}\left| {\psi '} \right\rangle \left\langle {\psi '} \right|\\{e^{i{{\hat H}^\dagger }_{eff}\delta t}} \otimes \left| 1 \right\rangle \left\langle 1 \right|\end{array}\]

So, the output mode has probability \sim {\Gamma _1}\delta t per \delta t of regressing back to the ground state, while the system state continues to evolve in accordance with the effective Hamiltonian {\hat H_{eff}}.

Hence, we have a near-unity probability of the external mode returning to the ground state within a time of order 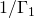1/{\Gamma _1}, thus we can sum over all histories in which the photon is absorbed within this time and again this matches the quantum jump trajectories exactly

Generalizing, the probability of such histories will be exactly of the form:

    \[\begin{array}{l}{\left( {2\delta t{\kappa ^2}/G} \right)^N}{\rm{Tr}}\left\{ {{e^{ - i{{\tilde H}_{eff}}\left( {T - {t_N}} \right)}}} \right. \cdot \\\hat a{e^{ - i{{\hat H}_{eff}}}}\left( {{t_N} - {t_{N - 1}}} \right)\hat a...\,\hat a{e^{ - i{{\hat H}_{eff}}t}}\\ \times \left| {\psi _t^{S,m,c}} \right\rangle \left\langle {\psi _t^{S,m,c}} \right|{e^{i{{\tilde H}^\dagger }_{eff}{t_1}}}{{\hat a}^\dagger }...\,\left. {{{\hat a}^\dagger }{e^{i{{\tilde H}^\dagger }_{eff}\left( {T - {t_N}} \right)}}} \right\}\end{array}\]

To decohere histories, the following must hold, for \varepsilon \ll 1:

    \[{\left| {\tilde D\left[ {h,h'} \right]} \right|^2} < {\varepsilon ^2}\tilde D\left[ {h,h'} \right] = {\varepsilon ^2}p(h)p(h')\]

for each separate h, h'. Hence, it suffices to analyze two histories which differ at a single time {t_i}, one with projection {\hat P_0}, the other {\hat P_1},

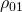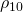which  is equivalent to picking out the {\rho _{01}} and {\rho _{10}} component of 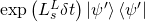\exp \left( {L_s^L\delta t} \right)\left| {\psi '} \right\rangle \left\langle {\psi '} \right| at that time

arriving at:

    \[\frac{{{{\left| {\tilde D\left[ {h,h'} \right]} \right|}^2}}}{{p(h)p(h')}} \sim \frac{1}{{{{\left( {G\delta t} \right)}^2}}}\]

with the sum rules given by O\left( {1/G\delta t} \right).

Concluding then, we have demonstrated that continuous measurements are given by the set of quantum jump trajectories corresponding to a set of decoherent histories that reproduces quantum mechanics as a Bayesian theory over Hilbert space with complex ring.

previously

previously

A Weyl-Plebanski 7-D Embedding of General Relativity
up next

up next

Deriving 4D De Sitter Space from T-Branes via D7-Brane Action
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on
1 Response