I will show that there is a quantum description of supersymmetric field theory that maps, via the quantum master equation, the two generating functionals, one linear, the other non-linear, of the extended actions of the superfield/super-antifield BRST formalism. It is key to note that local supersymmetric fields analytically entail that space-time has Sasaki-Einstein-curvature. Here is the central action for the supersymmetric field theory:
with the super-covariant derivatives of
![]()
are defined by:
![]()
and
![]()
and the super-derivative is:
![]()
where the Ashtekar-Barbero connection ![]() , for a, b = 1, 2, 3, is given in terms of co-triads
, for a, b = 1, 2, 3, is given in terms of co-triads ![]() thusly:
thusly:
![]()
and ![]() satisfying
satisfying
![]()
and the extrinsic curvature ![]() being:
being:
![]()
with the total action given by:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{S_T} = {S_0} + \sum\limits_\nu {\int {d\phi } } \left[ {{{\tilde D}^2}} \right.\left\{ {{B_i}} \right.\left( \wp \right){{\tilde D}^a}\Gamma _a^i\left( \wp \right)\\ + \,{{\bar c}_i}\left( \wp \right){{\tilde D}^a}{\nabla _a}{c^i}{\left. {\left. {\left( \wp \right)} \right\}} \right]_{\left| {_G} \right.}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a80af979157c2124266c594ff51911f5_l3.png)
with ![]() the Grassmannian variable describing a space with supersymmetric degrees of freedom at
the Grassmannian variable describing a space with supersymmetric degrees of freedom at ![]() and mini-superspace variables
and mini-superspace variables ![]() and
and ![]() the mini-superspace covariant derivative with the 4-D metric being:
the mini-superspace covariant derivative with the 4-D metric being:
![]()
where the field-strength for a matrix valued spinor field ![]() is given by
is given by
![]()
Thus, the action 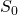 is invariant under the following gauge transformations
is invariant under the following gauge transformations
![]()
![]()
![]()
where ![]() is the infinitesimal bosonic transformation.
is the infinitesimal bosonic transformation.
Here is a serious problem: this gauge symmetry, in the path-integral formalism, implies that there exists infinitely many
![]()
that are physically equivalent to ![]() , and hence, divergences in the functional integral. To quantize such a theory, we must eliminate redundant gauge degrees of freedom and work with the Faddeev-Popov gauge condition:
, and hence, divergences in the functional integral. To quantize such a theory, we must eliminate redundant gauge degrees of freedom and work with the Faddeev-Popov gauge condition:
![]()
which yields, given the linearised gauge-fixing action corresponding to the above Faddeev-Popov gauge condition together with the induced ghost term:
with ![]() being the Nakanishi-Lautrup external superfield,
being the Nakanishi-Lautrup external superfield, ![]() and
and ![]() the ghost and antighost superfields in that order and
the ghost and antighost superfields in that order and ![]() the Slavnov-variation. In such a gauge, the total effective action for supersymmetric field theory is:
the Slavnov-variation. In such a gauge, the total effective action for supersymmetric field theory is:
![]()
and in order to be an integrable system, the Landau gauge
![]()
consequently must be imposed and therefore, the total action becomes, as required:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{S_T} = {S_0} + \sum\limits_\nu {\int {d\phi } } \left[ {{{\tilde D}^2}} \right.\left\{ {{B_i}} \right.\left( \wp \right){{\tilde D}^a}\Gamma _a^i\left( \wp \right) + \\{{\bar c}_i}\left( \wp \right){{\tilde D}^a}{\nabla _a}{c^i}{\left. {\left. {\left( \wp \right)} \right\}} \right]_{\left| {_G} \right.}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e46f3f4015a4aaa3e0063a7441bccee9_l3.png)
Now, the Curci-Ferrari non-linear gauge forces us to perform a shift in auxiliary superfield:
![]()
giving us the total effective action corresponding to the above non-linear gauge:
and both are are invariant under the third-quantized infinitesimal BRST transformations:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\delta _b}{\Omega ^i}\left( \wp \right) = if_{kj}^i{c^k}\left( \wp \right){\Omega ^j}\left( {\wp \delta \lambda } \right)}\\{{\delta _b}{\Omega ^{i\dagger }}\left( \wp \right) = - if_{kj}^i{\Omega ^{\dagger k}}\left( \wp \right){c^j}\left( \wp \right)\delta \lambda }\\{{\delta _b}{c^i}\left( \wp \right) = \frac{1}{2}f_{kj}^i{c^k}\left( \wp \right){c^j}\left( \wp \right)\delta \lambda }\\{{\delta _b}\Gamma _a^i\left( \wp \right) = {\nabla _a}{c^i}\left( \wp \right)\delta \lambda }\\{{\delta _b}{{\bar c}^i}\left( \wp \right) = {B^i}\left( \wp \right)\delta \lambda }\\{{\delta _b}{B^i}\left( \wp \right) = 0}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6fcf4d67d1d6278466aaf78f1a1d6c03_l3.png)
and crucial, ![]() being an infinitesimal anticommuting space-time independent parameter. Hence, we have nilpotency of order two. By using the BRST transformation, the sum of gauge-fixing as well as ghost parts of:
being an infinitesimal anticommuting space-time independent parameter. Hence, we have nilpotency of order two. By using the BRST transformation, the sum of gauge-fixing as well as ghost parts of:
we get a reduction to
![]()
with
![]()
Let us transition to the superfield/super-antifield formalism
Here, we find that the functional for the supersymmetric field theory in Landau type gauge is given by:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{Z_L}\left[ 0 \right] = \int {\not D} M{e^{ - {W_L}\left[ {\Phi ,{\Phi ^ * }} \right]}} = \\\int {\not DM\exp \left[ { - \left( {{S_0}} \right.} \right.} + \sum\limits_\nu {\int {d\phi } } \left[ {\Gamma _{1i}^{a * }} \right.\\ \cdot {\nabla _a}{c^i} + c_{1i}^ * f_{kj}^i{c^k}{c^j} + \bar c_{1i}^ * \left. {\left. {{{\left. {{B^i}} \right]}_{\left| {_G} \right.}}} \right)} \right]\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5dbe782b24f7ddce1610dda6f1ffb1a3_l3.png)
with ![]() the extended supersymmetric quantum action.
the extended supersymmetric quantum action.
The fermionic sector for the supersymmetric field theory in Landau-gauge becomes
![]()
‘Solving’ for super-antifields for the corresponding Landau gauge yields:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\Omega _1^{i * } = \frac{{\delta \,{\Psi _L}}}{{\delta \,{\Omega _i}}} = 0}\\{\Omega _1^{i\dagger * } = \frac{{\delta \,{\Psi _L}}}{{\delta \,\Omega _i^\dagger }} = 0}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-315d30216c7d819cb9656c52fa598f96_l3.png)
![]()
and
![]()
Thus the generating functional for supersymmetric field theory in non-linear gauge of superfields/super-antifields is:
and so the fermionic gauge-fixing for the non-linear gauge is:
and the corresponding super-antifields gauge-fixing fermionic system becomes:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\Omega _2^{i * } = \frac{{\delta \,{\Psi _{NL}}}}{{\delta \,{\Omega _i}}} = 0}\\{\Omega _2^{i\dagger * } = \frac{{\delta \,{\Psi _{NL}}}}{{\delta \,\Omega _i^\dagger }} = 0}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bcf0fb3f4a009940847e7fd6fb58f58f_l3.png)
![]()
![]()
and
![]()
Now it becomes clear what the difference between the non-linear and linear extended quantum actions:
and we can now arrive at the structural form of solutions to the quantum master equation:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\Delta {e^{i{W_\Psi }\left[ {\Phi ,{\Phi ^ * }} \right]}} = 0}\\{\Delta \equiv {{\left( { - 1} \right)}^\varepsilon }\frac{{{{\not \partial }_l}}}{{\not \partial \Phi }}\frac{{{{\not \partial }_l}}}{{\not \partial {\Psi ^ * }}}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-600fb756a251fa12f05d0c8578d18a73_l3.png)
which has the form:
![]()
We are now in a position to establish a map between the two generating functionals corresponding to the above extended actions by use of the superfield/super-antifield dependent BRST transformations
The superfield/super-antifield dependent BRST transformation yields the following Jacobian functional measure:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{{Z'}_L}\left[ 0 \right] = \int {\not D} M\left( {s{\rm{Det}}J\left[ {\Phi ,{\Phi ^ * }} \right]} \right) \cdot \\\exp \left\{ { - {W_L}\left[ {\Phi ,{\Phi ^ * }} \right]} \right\} = \\\int {\not D} M{e^{ - \left( {{W_L}\left[ {\Phi ,{\Phi ^ * }} \right] - is{\rm{Tr}}\,{\rm{In}}J\left[ {\Phi ,{\Phi ^ * }} \right]} \right)}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6f5f81c0ab5908305a7f5e7117d4280b_l3.png)
with ![]() referring to the Jacobian change of variables. The associated matrix for the superfield/super-antifield dependent BRST transformation is therefore:
referring to the Jacobian change of variables. The associated matrix for the superfield/super-antifield dependent BRST transformation is therefore:
By BRST-nilpotency, we get a reduction to:
![]()
thus simplifying our Jacobian functional measure:
![]()
Hence, the Slavnov variation yields:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{s_b}\Lambda \left[ {\Phi ,{\Phi ^ * }} \right] = \sum\limits_\nu {\int {d\phi \exp \left( { - i} \right.} } \\\left[ {c_{2i}^ * \left( \wp \right)\left( {\frac{1}{2}f_{kj}^i{c^k}\left( \wp \right){c^j}\left( \wp \right)} \right)} \right. + \\\left( {\bar c_{2i}^ * \left( \wp \right) - \bar c_{1i}^ * \left( \wp \right)} \right){\left. {\left. {{B^i}\left( \wp \right)} \right]} \right)_{\left| {_G} \right.}} - 1\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f046778c7d1c1b610e03f4d354b86651_l3.png)
therefore, by Jacobian change of variables and BRST-nilpotency, we get our all too important map
![]()

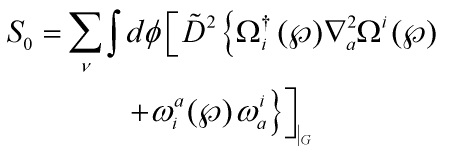
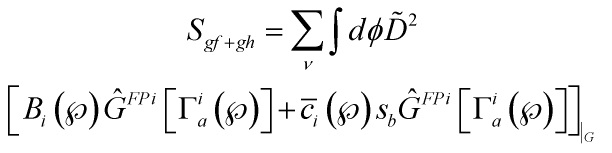
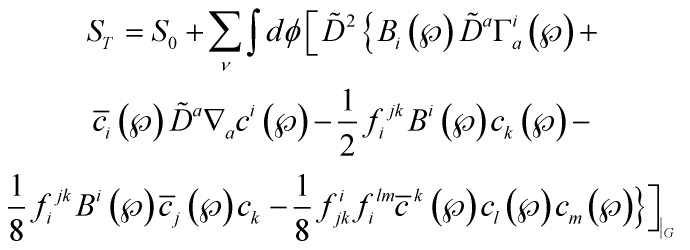
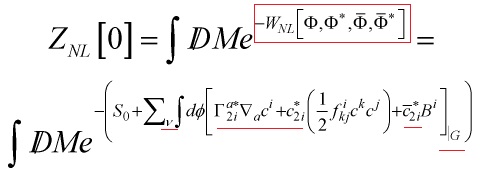
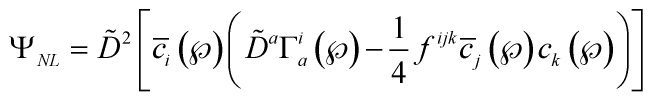
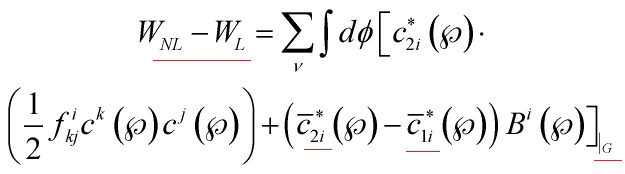
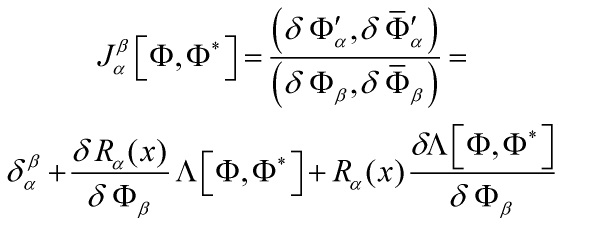



1 Response
The Quantum Master Equation and Supersymmetric-Field-Cosmology
Saturday, September 24, 2016[…] definitions of terms, see my 'SuperSymmetric Field Theory and the Quantum Master Equation' post. Some philosophical points are in order […]