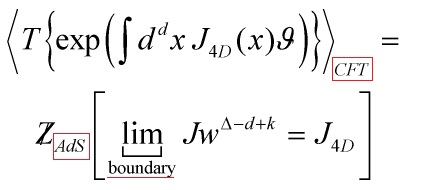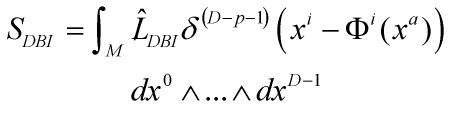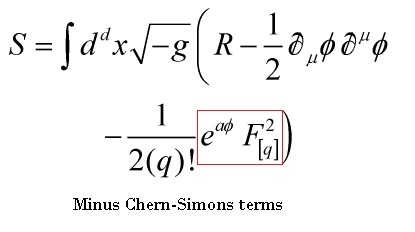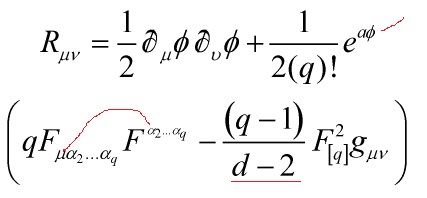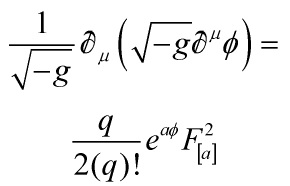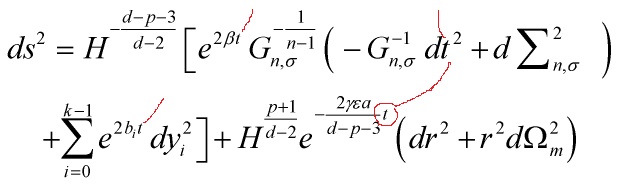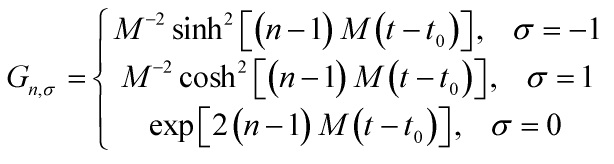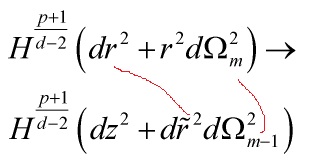Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

The AdS/CFT Duality, Time, and Spacelike Branes

By Posted on In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Super String Theory, Time, Witten Theory ,
photo

I will discuss one of the deepest aspects of string/M-theory, namely the AdS/CFT duality, expressed as

 

eq1

and spacelike branes, whose action is generally of the form

    \[S = {S_0} = \int {d{x^0}} {d^p}x\sqrt { - 1 + E_{p + 1}^2 + {{\dot \tau }^2}} \]

which is i time the Dirac-Born-Infeld action

 

eq2

 

over the target space M and

    \[{\delta ^{\left( {D - p - 1} \right)}}\left( {{x^i} - {\Phi ^i}({x^a})} \right)\]

is a Dirac delta function interpreted as a distribution along {x^i} directions, and briefly discuss cosmological singularities. This is an excellent read on S-branes. It is folklore knowledge that any Minkowskian geometry of the worldvolume of a p-brane can be replaced with any Ricci-flat spacetime with  Kasner-time-dependence and satisfying the Dp-brane worldvolumes can be replaced by a Friedmann-Robertson-Walker metric with a conformal factor. It can be shown that there is a deep mathematical relation between p-branes and chargeless S-brane worldvolume backgrounds related the via AdS/CFT duality with a Maldacena deformation satisfying U-duality.

The d-dimensional Einstein frame action describing bosonic sectors of supergravity theories containing the graviton, {g_{MN}}, the dilaton \phi coupled to the q-form field strength

    \[{F_{\left[ q \right]}} = d{A_{\left[ {q - 1} \right]}}\]

with the coupling constant a is given as

 

eq3

 

with the field equations:

 

eq4

 

    \[{\not \partial _\mu }\left( {\sqrt { - g} {e^{a\phi }}{F^{\mu {\nu _2}...{\nu _q}}}} \right) = 0\]

and

 

eq5.1

 

and the field strength satisfying the Bianchi identity

    \[{\not \partial _{\left[ {\upsilon {F_{{\mu _1}}}{{...}_{{\mu _q}}}} \right]}} = 0\]

 

It is solutions that describe a p-brane in the presence of a chargeless S-brane without any smearing in p-brane’s transverse space that is central, and here is where time comes in, as I will show that

 

eq6

 

    \[\left\{ {\begin{array}{*{20}{c}}{\phi = \varepsilon a{\rm{In}}H + \gamma t}\\{{F_{t1...pr}} = {Q^ * }\left[ {Vol\left( {{\Omega _m}} \right)} \right]\left( E \right)}\\{{F_{1...m}} = Q\,vol\left( {{\Omega _m}} \right)\left( M \right)}\end{array}} \right.\]

with vol\left( {{\Omega _m}} \right) being the volume form of the m-dimensional unit sphere {{\Omega _m}} and ‘*‘ the Hodge dual operation with respect to full metric. Note now that in the metric above,

    \[d\Sigma _{n,\sigma }^2\]

represents the metric on the n-dimensional unit hyperbola, unit sphere or flat space and the function {G_{n,\sigma }} is given as

 

eq7

G

 

and our constants do satisfy

    \[\beta = - \frac{1}{{n - 1}}\left( {\sum\limits_{i = 0}^{k - 1} {{b_i} - \frac{{\left( {m + 1} \right)\gamma \varepsilon a}}{{d - p - 3}}} } \right)\]

    \[\begin{array}{c}n\left( {n - 1} \right){M^2} = \left( {n - 1} \right){\beta ^2} + \\\sum\limits_{i = 0}^{k - 1} {b_i^2} + + \frac{{\left( {m + 1} \right){\gamma ^2}{a^2}}}{{{{\left( {d - p - 3} \right)}^2}}} + \frac{{{\gamma ^2}}}{2}\end{array}\]

Deep: if one sets all time-dependent parts to zero, the solution is exactly the p-brane solution

and the dilaton coupling ‘a‘ is zero in 11-D SUGRA and in type IIA and IIB SUGRAs, it is given by

    \[\left\{ {\begin{array}{*{20}{c}}{\varepsilon a = \frac{{3 - p}}{2}{\rm{ RR - branes}}}\\{\varepsilon a = \frac{{p - 3}}{2}{\rm{ NS - branes}}}\end{array}} \right.\]

Thus, the solution below

    \[\left\{ {\begin{array}{*{20}{c}}{\phi = \varepsilon a{\rm{In}}H + \gamma t}\\{{F_{t1...pr}} = {Q^ * }\left[ {Vol\left( {{\Omega _m}} \right)} \right]\left( E \right)}\\{{F_{1...m}} = Q\,vol\left( {{\Omega _m}} \right)\left( M \right)}\end{array}} \right.\]

can be interpreted as a superposition of a p-brane with a chargeless S-brane

Now note that one of the constants \left\{ {M,\beta ,\gamma ,{b_i}} \right\} can be set to 1 by rescaling the time coordinate. There are generic singularities as t \to \pm \infty, as can be seen from the collapse of parts of the metric functions. When t is finite, time-dependent metric functions are well-behaved except for the {G_{n, - 1}} function G above, which ought and does become zero at t = {t_0}.

However, and that is the deep point, this is not a singularity

since one can always define a new coordinate

    \[u = {\left( {t - {t_0}} \right)^{ - 1/2}}\]

thus getting

    \[ - d{u^2} + {u^2}{\Sigma _{n, - 1}}\]

which is exactly the flat spacetime in Rindler-coordinates. So, for \sigma = - 1, one gets

    \[\left\{ {\begin{array}{*{20}{c}}{t \in \left( {{t_0},\infty } \right)}\\{{\rm{or}}}\\{t \in \left( { - \infty ,{t_0}} \right)}\end{array}} \right.\]

and for \sigma = \left\{ {0,1} \right\}, we get

    \[t \in \left( { - \infty ,\infty } \right)\]

and for the general solution

    \[\left\{ {\begin{array}{*{20}{c}}{\phi = \varepsilon a{\rm{In}}H + \gamma t}\\{{F_{t1...pr}} = {Q^ * }\left[ {Vol\left( {{\Omega _m}} \right)} \right]\left( E \right)}\\{{F_{1...m}} = Q\,vol\left( {{\Omega _m}} \right)\left( M \right)}\end{array}} \right.\]

we can smear some directions from the \left( {m + 1} \right)-replacement

 

eq8

 

with the harmonic function H now independent of z-coordinate.

Hence, we have Dp-and-Mq-brane solution in S-Dp-brane backgrounds with no singularity, ‘living’ in the bulk of

    \[Ad{S_7} \times {S^4}\]

satisfying singularity-free Friedmann-Robertson-Walker type time-dependent dynamics on the boundary

and this is deep, and to be continued, however, I must discuss the problem(s) of time in physics.

previously

The Witten Index and Integral Measure Analysis

up next

On the Problem of Time in Quantum Physics
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on