The Witten Index and Integral Measure Analysis

By George Shiber Wednesday, June 1, 2016Friday, October 26, 2018 In Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Physics, Super String Theory, Supersymmetry, Witten Theory lattice theory, path integrals

In my last post, I studied some aspects of Witten Index. Here, I shall probe ways of measuring the WI via integral analysis, as it plays a central role in supersymmetric Yang-Mills quantum theories with saturated and maximal SuSy. In the context of quantum mechanics, to get the path integral formulation from the operator formulation, one discretizes the temporal direction then injects a complete set at each of the time slice:

with ‘a’ being the lattice spacing. So for a bosonic dimensionless lattice field ${\phi ^{{\rm{lat}}}}$ , the path integral measure is

${\int {D\,\phi } ^{{\rm{lat}}}}\prod\limits_{k = 0}^{N - 1} {\left[ {\left( {\frac{1}{{2\pi }}} \right)\int_{ - \infty }^\infty {d\phi \,_k^{{\rm{lat}}}} } \right]}$

and in the fermionic variables case,

$\int {D{\psi ^ * }} D\psi \prod\limits_{k = 0}^{N - 1} {\int {d{\psi ^ * }} } d{\psi _k}$

which will allow us to derive and determine the natural-measure for the path integral. In lattice theory, we do no compute the integral nor integrate at all, rather carry an ensemble averages that yield the the ratios of the integration. A relation between the path integral regularized on the lattice and the ensemble averages. The expectation value in the path integral setting is

$\left\langle A \right\rangle = \frac{{\int {D\phi A{e^{ - S}}} }}{{\int {D\phi {e^{ - S}}} }}$

with $S$ the action of the system: note, the denominator above is exactly the Witten partition function which we are after for normalization analysis. The main problem though is that it is impossible to measure the partition function given that it is a ratio and does not depend on the normalization of the path integral. Let’s look at the following though:

with $\mu$ an arbitrary dimensionless parameter. Now, using the measure defined by the following equation:

$\int {D{\psi ^ * }} D\psi \prod\limits_{k = 0}^{N - 1} {\int {d{\psi ^ * }} } d{\psi _k}$

we get

(C)

with $\phi _i^{{\rm{lat}}} \to {\phi _i}$ . For any real value of $\mu$ , one can determine $C$ analytically to give the overall normalization of the path integral while realizing that $C$ is given just as an integration defined in (C) above.

The term:

$\left\langle {{e^{ + S}}{e^{ - 1/2\sum\nolimits_i {{\mu ^2}{{\left( {\phi _i^{{\rm{lat}}}} \right)}^2}} }}} \right\rangle$

is an ‘observable’ in the integral-measure computation and thus one can obtain the value of the partition function through the following

$Z = \int {D\phi {e^{ - S}}} = \frac{C}{{\left\langle {{e^{ + S}}{e^{ - 1/2\sum\nolimits_i {{\mu ^2}\phi _i^2} }}} \right\rangle }}$

After integrating out the fermions, we get

and

$S' = {S_B} - {\rm{In}}\left| {\det D} \right|$

is an effective action with the kernel $D$ of the fermion bilinear, and $\sigma \left[ D \right]$ is the complex phase of $\det D$ .

Hence, the configurations for the ensemble average are generated using the effective action 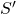$S'$ while ignoring the sign factor $\sigma \left[ D \right]$

Let ${\left\langle . \right\rangle _0}$ refer to the ensemble average over these configurations without the sign factor: so, the sign factor $\sigma \left[ D \right]$ ought to be reweighted in the measurement afterwards:

So, to determine the normalization of partition function, we must invert the effect of the sign factor in addition to the contribution from the effective action ${e^{ - S'}}$ , thus equation

becomes

where the numerator gives again the integration (C) above.

Hence, we finally get the expression for the Witten index 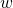$w$

$w = {Z_P} = C\frac{{{{\left\langle {\sigma \left[ {{D_P}} \right]} \right\rangle }_{0,P}}}}{{{{\left\langle {e_P^{S' - 1/2\sum\nolimits_i {{\mu ^2}\phi _i^2} }} \right\rangle }_{0,P}}}}$

given that all the fields are imposed the periodic boundary conditions as indicated by the suffix P. Now, with $\varphi$ a pseudo fermion, one can rewrite

$w = {Z_P} = C\frac{{{{\left\langle {\sigma \left[ {{D_P}} \right]} \right\rangle }_{0,P}}}}{{{{\left\langle {e_P^{S' - 1/2\sum\nolimits_i {{\mu ^2}\phi _i^2} }} \right\rangle }_{0,P}}}}$

in the following way: since the definition of the measure gives exactly

with:

$\varphi = \frac{1}{{\sqrt 2 }}\left( {{\varphi ^{(1)}} + i{\varphi ^{(2)}}} \right)$

So, one can obtain the expression for the Witten index as

$w = {Z_P} = C{C_\varphi }\frac{{{{\left\langle {\sigma \left[ {{D_P}} \right]} \right\rangle }_{0,p}}}}{{{{\left\langle {e_P^{S'' - \sum\nolimits_i {{\mu ^2}\phi _i^2\varphi _i^ * {\varphi _j}} }} \right\rangle }_{0,P}}}}$