Randall-Sundrum Compactification Models and Bulk-Field Actions

By George Shiber Thursday, April 21, 2016Saturday, August 17, 2019 In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Philosophy Of Science, Physics, Super String Theory Branes, bulk-field action

The key to absorbing this post, following my last two, is to appreciate that the Standard Model ‘particles’/fields can be interpreted as low-lying Kaluza-Klein excitations of Randall-Sundrum bulk fields (see header photo). To carry out a Horava-Witten decomposition, flesh out the bulk-field as

$\Phi \left( {x,\phi } \right) = \sum\limits_n {{\psi _n}} \frac{{{y_n}\left( \phi \right)}}{{\sqrt {{r_c}} }}$

with ${y_n}\left( \phi \right)$ satisfying

$\int\limits_{ - 1\pi }^\pi {d\phi {e^{ - 2\sigma (\phi )}}} {y_n}\left( \phi \right){y_m}\left( \phi \right) = {\delta _{nm}}$

and the action is then given by

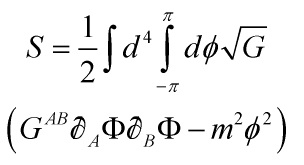
Eq. 1

After an integration by parts and substituting-in ${e^{ - 2\sigma \left( \phi \right)}}$ , Eq. 1 reduces to

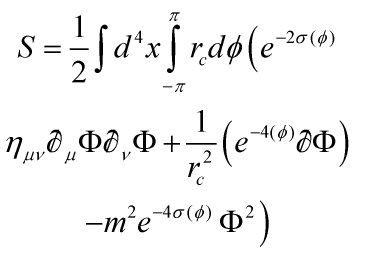
Eq. 2

Now, as in typical Kaluza-Klein compactifications, the bulk field $\Phi \left( {x,\phi } \right)$ manifests itself to a four-dimensional ‘observer’ as an infinite tower of scalars ${\psi _n}(x)$ with masses ${m_n}$ . After changing variables to

$\left\{ {\begin{array}{*{20}{c}}{{z_n} = {m_n}{e^{\sigma \left( \phi \right)}}/k}\\{{f_n} = {e^{ - 2\sigma \left( \phi \right)}}{y_n}}\end{array}} \right.$

we get

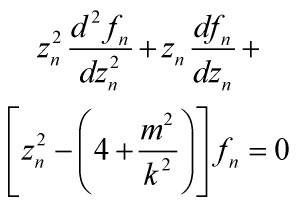
Eq. 3

Bessel functions of order

$v = \sqrt {4 + \frac{{{m^2}}}{{{k^2}}}}$

give the standard Bertotti-Robinson-solutions. Hence, we have

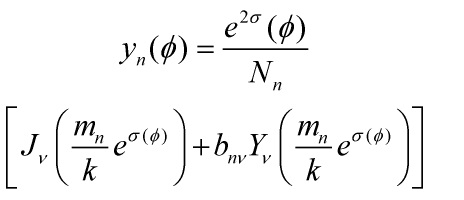
Eq. 4

with ${N_n}$ a normalization factor. That the differential operator on the LHS of

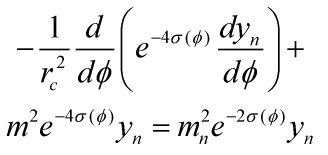
Eq. 5

is self-adjoint means that the derivative of ${y_n}\left( \phi \right)$ is continuous at the orbifold fixed points, and that gives us two relations that can solve for ${m_n}$ and ${b_{n\nu }}$ , yielding

${b_{n\nu }} = \frac{{2{J_\nu }\left( {\frac{{{m_n}}}{k}} \right){{J'}_\nu }\left( {\frac{{{m_n}}}{k}} \right)}}{{2{Y_\nu }\left( {\frac{{{m_n}}}{k}} \right){{Y'}_\nu }\left( {\frac{{{m_n}}}{k}} \right)}}$

Now let

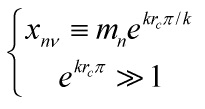
Cnd. 1

and so we have

$2{J_\nu }\left( {{x_{n\nu }}} \right) + {x_{n\nu }}{J'_\nu }\left( {{x_{n\nu }}} \right) = 0$

The exponential suppression can be understood from Eq. 4 above: the modes ${y_n}\left( \phi \right)$ are larger near the 3-brane at $\phi = \pi$ , therefore we can expect to find the Kaluza-Klein excitations in that region and their masses behave exactly in the same way as masses of fields confined to the brane at $\phi = \pi$ . For the massless case, m = 0, there is a mode with ${y_1}$ constant and ${x_{12}} = 0$ and can be obtained from Eq. 4 and Eq. 5 above. For ${x_{1\nu }}$ small, we get

${x_{1\nu }} \simeq \frac{1}{{\sqrt 2 }}\left( {\frac{m}{k}} \right){e^{k{r_c}\pi }}$

Without loss of generality or substance, I will assume $m/k$ is of order unity, yielding us

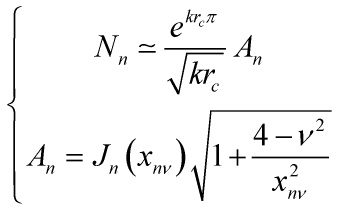
Cnd. 2

Four-dimensionally, these induce couplings between the Kaluza-Klein modes and so the exponential factor in

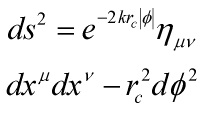
Eq. 6

where ${x^\mu }$ are Lorentz coordinates on the four-dimensional surfaces of constant $\phi$ , plays an essential role in determining the effective scale of the couplings. If the Planck scale sets the scale of the five-dimensional couplings, the low-lying Kaluza-Klein modes will have TeV-range self-interactions!

Start with the term-action

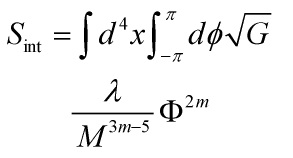
Eq. 7

where $\lambda$ is of order unity. Then, mode expansion gives us the self-interactions of the light Kaluza-Klein states

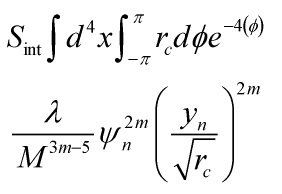
Eq. 8

Thus, the effective 4-D coupling constants for the $\psi _n^{2m}$ interactions are

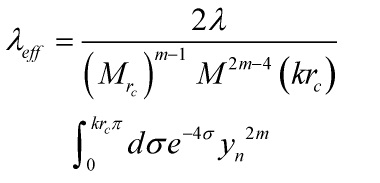
Eq. 9

By Horava-Witten bulk-term derivation, Eq. 7 and Eq. 8 become, respectively, Eq. 10 and 11:

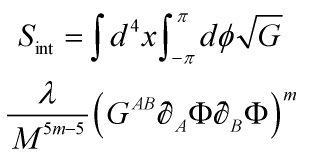
Eq. 10

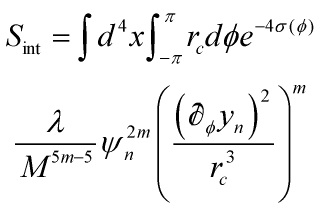
Eq. 11

So, from a 4-D ‘observers-perspective’, we get a $\psi _n^{2m}$ interaction with a coupling constant

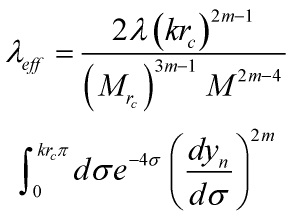
Eq. 12

and for ‘large’ $k{r_c}$ , it reduces to

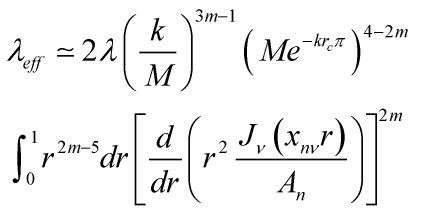
Eq. 13

And the philosophically deep point is that in both cases, the scale relevant to four-dimensional physics is not $M$ , but

$\nu = M{e^{ - k{r_c}\pi }}$

Thus in the Randall-Sundrum compactification model, bulk scalars acquire low lying Kaluza-Klein modes with four-dimensional masses of order the weak scale and four-dimensional non-renormalizable interactions that are suppressed by powers of the weak scale even though from a five-dimensional brane-perspective their masses and interactions are characterized by the Planck scale, and thus establishes the points of my last three posts relating brane-based cosmology, the Randall–Sundrum model and Klebanov-Strassler warped space-time geometry.

B1y-63BIIAALr-T